Energy Demand Estimation with PSO Algorithm
Categorized under My Projects Last modified at:
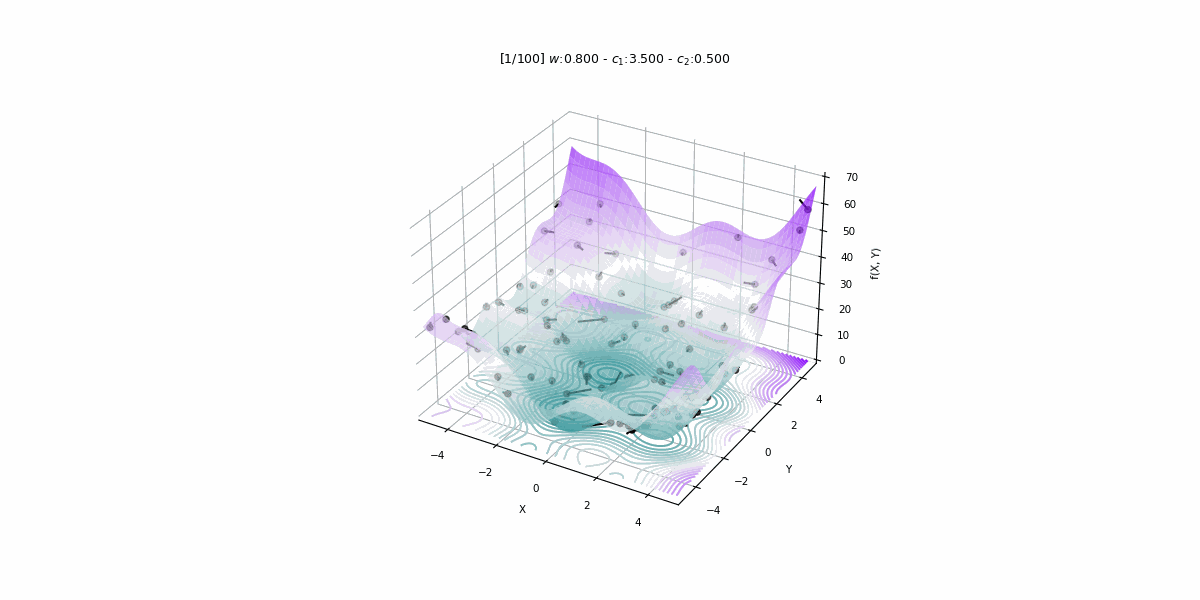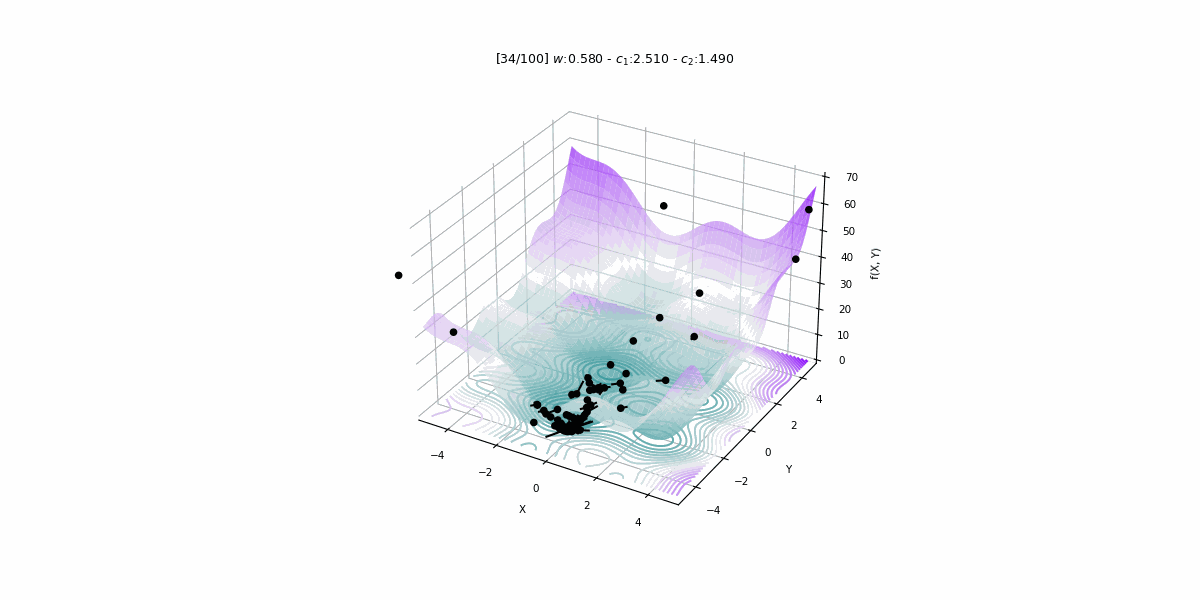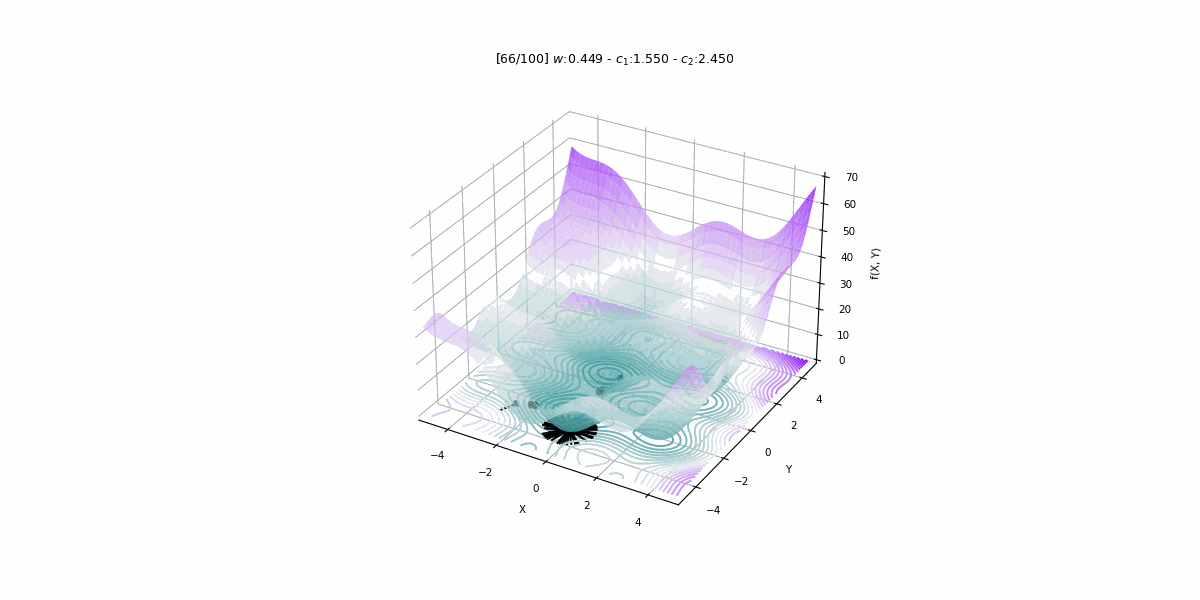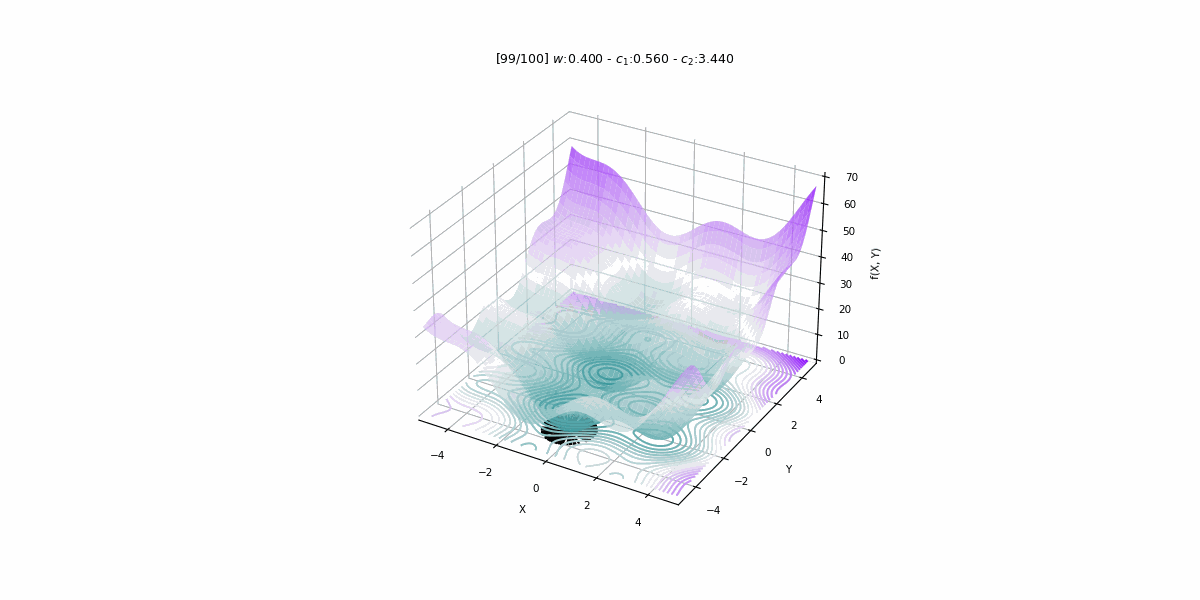
PSO algoritması ile enerji talebi tahmini
- Linear Model
- Download and install libraries
- Import the necessary libraries
- Dataset
- Load Data
- Describe the dataset
- Graphical Analysis of Data
- Split Data
- PSO Algorithm
- Create PSO Model
- Run PSO
Bu projede 1979 – 2015 yıllarına ait veriler kullanılarak Türkiye’nin enerji talebini PSO algoritması ile tahmin eden doğrusal bir tahmin modeli geliştirilmiştir.
Linear Model
\[E_{lineer}=w_1*X_1+w_2*X_2+w_3*X_3+w_4*X_4+w_5\]- X1 : GSYH
- X2 : Nüfus
- X3 : İthalat
- X4 : İhracat
Y : Enerji Talebi
- weights = [w1, w2, w3, w4, w5]
Download and install libraries
$ pip install matplotlib
$ pip install numpy
$ pip install pandas
$ pip install seaborn
Import the necessary libraries
from pso import PSO
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
Dataset
Load Data
data = pd.read_csv("dataset.csv")
print(data.head(5))
Yıl GSYH Nüfus İthalat İhracat Enerji_Talebi
0 1979 81 43.530 5.07 2.26 30.25
1 1980 68 44.438 7.91 2.91 31.45
2 1981 71 45.540 8.93 4.70 31.71
3 1982 64 46.688 8.84 5.75 33.70
4 1983 60 47.864 9.24 5.73 35.68
Describe the dataset
print(data.describe())
Yıl GSYH Nüfus İthalat İhracat Enerji_Talebi
count 37.000000 37.000000 37.000000 37.000000 37.000000 37.000000
mean 1997.000000 296.405405 62.397973 78.330000 49.741351 70.097297
std 10.824355 265.358820 10.533688 82.339139 52.341555 28.906369
min 1979.000000 59.000000 43.530000 5.070000 2.260000 30.250000
25% 1988.000000 90.000000 53.715000 14.340000 11.620000 47.290000
50% 1997.000000 181.000000 62.697000 41.400000 26.260000 70.200000
75% 2006.000000 400.000000 71.789000 139.580000 85.530000 93.150000
max 2015.000000 820.000000 77.695000 251.650000 157.610000 128.810000
print(data.shape)
(37, 6)
print(data.info())
RangeIndex: 37 entries, 0 to 36
Data columns (total 6 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Yıl 37 non-null int64
1 GSYH 37 non-null int64
2 Nüfus 37 non-null float64
3 İthalat 37 non-null float64
4 İhracat 37 non-null float64
5 Enerji_Talebi 37 non-null float64
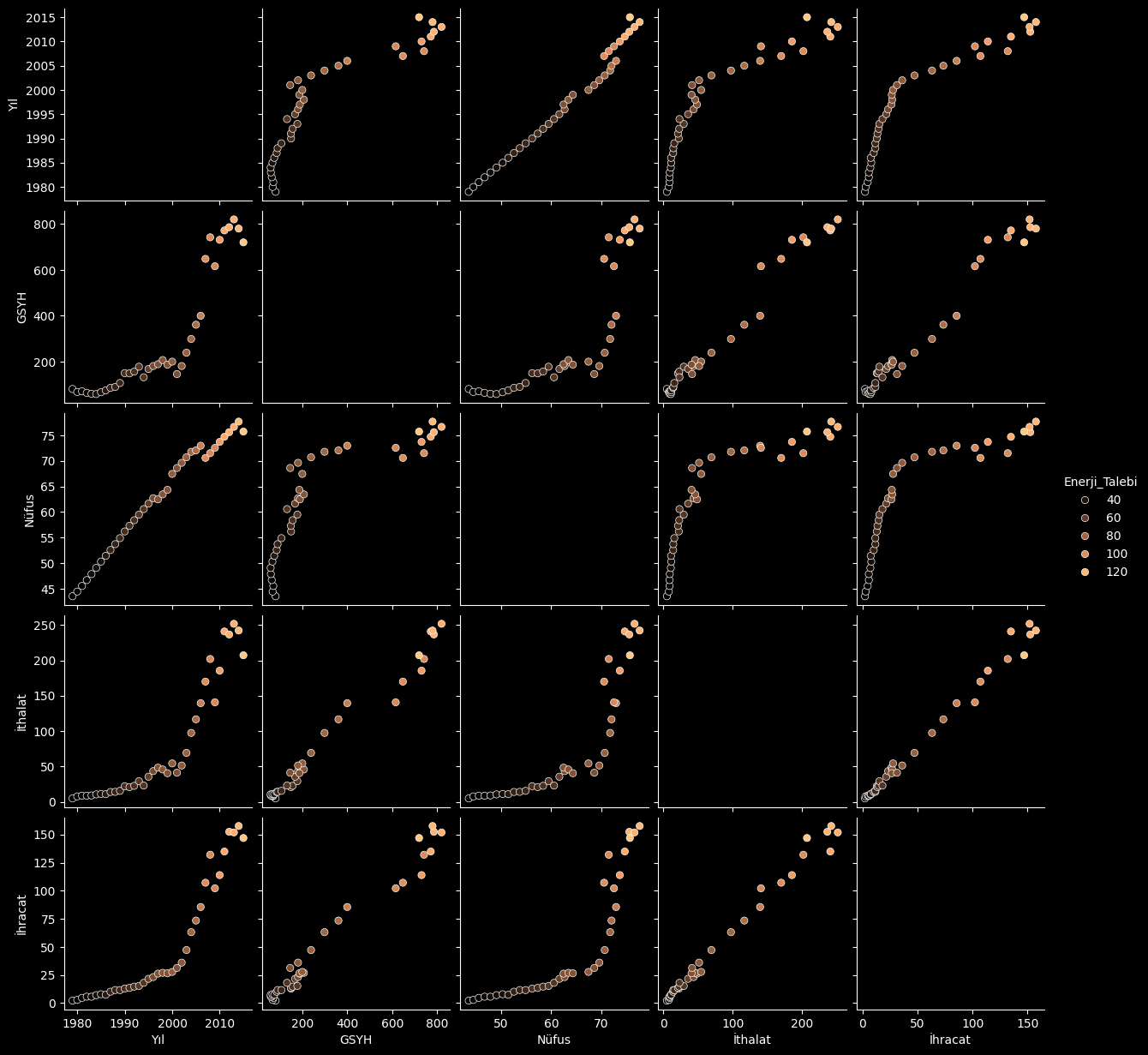
Graphical Analysis of Data
sns.pairplot(data=data, diag_kind='kde', hue='Enerji_Talebi',palette='copper')
plt.show()
Split Data
X = data.iloc[:, 1:-1].values # Features
Y = data.iloc[:, -1].values # Target
print(X.shape)
print(Y.shape)
(37, 4)
(37,)
PSO Algorithm
# file: "pso.py"
################################################################################
# #
# PSO (PARTICLE SWARM OPTIMIZATION) #
# PYTHON 3.13.0 #
# #
################################################################################
####################### IMPORT DEPENDENCIES ################################
import numpy as np
import matplotlib.pyplot as plt
########################### PARTICLE CLASS ###################################
class Particle:
def __init__(self, n=2, vmax=1, X0=None, bound=None):
"""
PARAMETERS:
n: TOTAL DIMENSIONS
vmax: MAXIMUM LIMITED VELOCITY OF A PARTICLE
X0: INITIAL POSITION OF PARTICLE SPECIFIED BY USER
bound: AXIS BOUND FOR EACH DIMENSION
################ EXAMPLE #####################
If X = [x,y,z], n = 3 and if
bound = [(-5,5),(-1,1),(0,5)]
Then, x∈(-5,5); y∈(-1,1); z∈(0,5)
##############################################
X: PARTICLE POSITION OF SHAPE (n,1)
V: PARTICLE VELOCITY OF SHAPE (n,1)
pbest: PARTICLE'S OWN BEST POSITION OF SHAPE (n,1)
"""
# IF INITIAL POSITION 'X0' IS NOT SPECIFIED THEN DO RANDOM INITIALIZATION OF 'X'
if X0 is None:
self.X = 2 * np.random.rand(n, 1) - 1
else:
self.X = np.array(X0, dtype="float64").reshape(-1, 1)
self.bound = bound
self.n = n
self.vmax = vmax
"""
np.random.rand() ∈ (0,1)
THEREFORE 2*vmax*np.random.rand() ∈ (0,2*vmax)
THUS, V = 2*vmax*np.random.rand() - vmax ∈ (-vmax,vmax)
"""
self.V = 2 * vmax * np.random.rand(n, 1) - vmax
self.clip_X()
# INITIALIZE 'pbest' WITH A COPY OF 'X'
self.pbest = self.X.copy()
def clip_X(self):
# IF BOUND IS SPECIFIED THEN CLIP 'X' VALUES SO THAT THEY ARE IN THE SPECIFIED RANGE
if self.bound is not None:
for i in range(self.n):
xmin, xmax = self.bound[i]
self.X[i, 0] = np.clip(self.X[i, 0], xmin, xmax)
def update_velocity(self, w, c1, c2, gbest):
"""
PARAMETERS:
w: INERTIA WEIGHT
c1: INDIVIDUAL COGNITIVE PARAMETER
c2: SOCIAL LEARNING PARAMETER
gbest: GLOBAL BEST POSITION (BEST POSITION IN GROUP) OF SHAPE (n,1)
ACTION:
UPDATE THE PARTICLE'S VELOCITY
"""
self.clip_X()
self.V = w * self.V # PARTICLE'S PREVIOUS MOTION
self.V += c1 * np.random.rand() * (self.pbest - self.X) # COGNITIVE VELOCITY
self.V += c2 * np.random.rand() * (gbest - self.X) # SOCIAL VELOCITY
self.V = np.clip(self.V, -self.vmax, self.vmax)
def update_position(self):
"""
ACTION:
UPDATE THE PARTICLE'S POSITION
"""
self.X += self.V
self.clip_X()
########################### PSO CLASS ####################################
class PSO:
def __init__(
self,
fitness,
P=30,
n=2,
w=0.72984,
c1=2.8,
c2=2.05,
Tmax=300,
vmax=1,
X0=None,
bound=None,
update_w=False,
update_c1=False,
update_c2=False,
update_vmax=False,
plot=False,
min=True,
verbose=False,
):
"""
THE SYMBOLS OR NOTATIONS WERE TAKEN FROM [1] AND [2]
PARAMETERS:
fitness: A FUNCTION WHICH EVALUATES COST (OR THE FITNESS) VALUE
P: POPULATION SIZE
n: TOTAL DIMENSIONS
w: INERTIA WEIGHT (CAN BE A CONSTANT OR CHANGES WITH ITERATION BASED ON 'update_w' VALUE)
update_w: BOOL VALUE (TRUE WHEN 'w' CHANGES WITH ITERATION AND FALSE IF 'w' IS CONSTANT)
c1: INDIVIDUAL COGNITIVE PARAMETER (CAN BE A CONSTANT OR CHANGES WITH ITERATION BASED ON 'update_c1' VALUE)
update_c1: BOOL VALUE (TRUE WHEN 'c1' CHANGES WITH ITERATION AND FALSE IF 'c1' IS CONSTANT)
c2: SOCIAL LEARNING PARAMETER (CAN BE A CONSTANT OR CHANGES WITH ITERATION BASED ON 'update_c2' VALUE)
update_c2: BOOL VALUE (TRUE WHEN 'c2' CHANGES WITH ITERATION AND FALSE IF 'c2' IS CONSTANT)
Tmax: MAXIMUM ITERATION
vmax: MAXIMUM LIMITED VELOCITY OF A PARTICLE (CAN BE A CONSTANT OR CHANGES WITH ITERATION BASED ON 'update_vmax' VALUE)
update_vmax: BOOL VALUE (TRUE WHEN 'vmax' CHANGES WITH ITERATION AND FALSE IF 'vmax' IS CONSTANT)
X0: INITIAL POSITION OF PARTICLE SPECIFIED BY USER
bound: AXIS BOUND FOR EACH DIMENSION
################ EXAMPLE #####################
If X = [x,y,z], n = 3 and if
bound = [(-5,5),(-1,1),(0,5)]
Then, x∈(-5,5); y∈(-1,1); z∈(0,5)
##############################################
plot: BOOL VALUE (TRUE IF PLOT BETWEEN GLOBAL FITNESS (OR COST) VALUE VS ITERATION IS NEEDED ELSE FALSE)
min: BOOL VALUE (TRUE FOR 'MINIMIZATION PROBLEM' AND FALSE FOR 'MAXIMIZATION PROBLEM')
verbose: BOOL VALUE (TRUE IF PRINTING IS REQUIRED TO SHOW GLOBAL FITNESS VALUE FOR EACH ITERATION ELSE FALSE)
"""
self.fitness = fitness
self.P = P
self.n = n
self.w = w
self.c1, self.c2 = c1, c2
self.Tmax = Tmax
self.vmax = vmax
self.X = X0
self.bound = bound
self.update_w = update_w
self.update_c1 = update_c1
self.update_c2 = update_c2
self.update_vmax = update_vmax
self.plot = plot
self.min = min
self.verbose = verbose
def optimum(self, best, particle_x):
"""
PARAMETERS:
best: EITHER LOCAL BEST SOLUTION 'pbest' OR GLOBAL BEST SOLUTION 'gbest'
particle_x: PARTICLE POSITION
ACTION:
COMPARE PARTICLE'S CURRENT POSITION EITHER WITH LOCAL BEST OR GLOBAL BEST POSITIONS
1. IF PROBLEM IS MINIMIZATION (min=TRUE), THEN CHECKS WHETHER FITNESS VALUE OF 'best'
IS LESS THAN THE FITNESS VALUE OF 'particle_x' AND IF IT IS GREATER, THEN IT
SUBSTITUTES THE CURRENT PARTICLE POSITION AS THE BEST (GLOBAL OR LOCAL) SOLUTION
2. IF PROBLEM IS MAXIMIZATION (min=FALSE), THEN CHECKS WHETHER FITNESS VALUE OF 'best'
IS GREATER THAN THE FITNESS VALUE OF 'particle_x' AND IF IT IS LESS, THEN IT
SUBSTITUTES THE CURRENT PARTICLE POSITION AS THE BEST (GLOBAL OR LOCAL) SOLUTION
"""
if self.min:
if self.fitness(best) > self.fitness(particle_x):
best = particle_x.copy()
else:
if self.fitness(best) < self.fitness(particle_x):
best = particle_x.copy()
return best
def initialize(self):
"""
PARAMETERS:
population: A LIST OF SIZE (P,) WHICH STORES ALL THE SWARM PARTICLE OBJECT
gbest: GLOBAL BEST POSITION (BEST POSITION IN GROUP) OF SHAPE (n,1)
ACTION:
FOR EACH PARTICLE 'i' IN SWARM POPULATION OF SIZE 'P'
1. IT INITIALIZE POSITION 'X' AND VELOCITY 'V' OF PARTICLE 'i' AND STORES IT IN 'population' LIST
2. INITIALIZE 'gbest' WITH COPY OF 'ith' PARTICLE'S POSITION 'X' HAVING BEST FITNESS
"""
self.population = []
for i in range(self.P):
self.population.append(
Particle(n=self.n, vmax=self.vmax, X0=self.X, bound=self.bound)
)
if i == 0:
self.gbest = self.population[0].X.copy()
else:
self.gbest = self.optimum(self.gbest, self.population[i].X)
def update_coeff(self):
"""
ACCORDING TO THE PAPER BY M. CLERC AND J. KENNEDY [3], TO DEFINE A STANDARD FOR PARTICLE SWARM OPTIMIZATION,
THE BEST STATIC PARAMETERS ARE w=0.72984 AND c1 + c2 >= 4. MORE EXACTLY c1 = 2.05 AND c2 = 2.05
BUT ACCORDING TO [2] SOME OTHER RESEARCHERS THOUGHT THAT c1 DID NOT EQUAL c2 , AND REACHED A CONCLUSION
c1 = 2.8 FROM EXPERIMENTS.
BASED ON THESE IDEAS AND INSPIRED BY THE PAPER BY G. SERMPINIS [5],
[6] SUGGEST THE UPDATION OF THE COEFFICIENTS (c1 AND c2) AS CODED HERE.
ADDITIONALLY, THE LINEAR DECAY OF THE PARAMETER 'w' WAS INITIALLY PROPOSED BY
YUHUI AND RUSS Y. H. SHI AND R. C. EBERHART [4].
CONCEPT OF UPDATING MAXIMUM VECOLITY IS ALSO AVAILABLE IN [2]
"""
if self.update_w:
self.w = 0.9 - 0.5 * (self.t / self.Tmax)
if self.update_c1:
self.c1 = 3.5 - 3 * (self.t / self.Tmax)
if self.update_c2:
self.c2 = 0.5 + 3 * (self.t / self.Tmax)
if self.update_vmax:
self.vmax = 1.5 * np.exp(1 - (self.t / self.Tmax))
def move(self):
"""
PARAMETERS:
t: ITERATION NUMBER
fitness_time: LIST STORING FITNESS (OR COST) VALUE FOR EACH ITERATION
time: LIST STORING ITERATION NUMBER ([0,1,2,...])
ACTION:
AS THE NAME SUGGESTS, THIS FUNCTION MOVES THE PARTICLES BY UPDATING THEIR
POSITION AND VELOCITY. ALSO BASED ON THE TYPE OF PROBLEM (MAXIMIZATION OR
MINIMIZATION), IT CALLS THE 'optimum' FUNCTION AND EVALUATE THE 'gbest'
AND 'pbest' PARAMETERS USING FITNESS VALUE. IT ALSO UPDATE THE COEFFICIENTS.
NOTE: THIS FUNCTION PRINTS THE GLOBAL FITNESS VALUE FOR EACH ITERATION
IF THE VERBOSE IS TRUE
FOLLOW [1] WHERE THE PSO ALGORITHM PSEUDO CODE IS PRESENT IN 'FIGURE-1'
"""
self.t = 0
self.fitness_time, self.time = [], []
while self.t <= self.Tmax:
self.update_coeff()
for particle in self.population:
particle.update_velocity(self.w, self.c1, self.c2, self.gbest)
particle.update_position()
particle.pbest = self.optimum(particle.pbest, particle.X)
self.gbest = self.optimum(self.gbest, particle.X)
self.fitness_time.append(self.fitness(self.gbest))
self.time.append(self.t)
if self.verbose:
print(
"Iteration: ",
self.t,
"| best global fitness (cost):",
round(self.fitness(self.gbest), 7),
)
self.t += 1
def execute(self):
"""
A KIND OF MAIN FUNCTION
PRINTS THE FINAL SOLUTION
"""
self.initialize()
self.move()
print("\nOPTIMUM SOLUTION\n >", np.round(self.gbest.reshape(-1), 7).tolist())
print("\nOPTIMUM FITNESS\n >", np.round(self.fitness(self.gbest), 7))
print()
if self.plot:
self.Fplot()
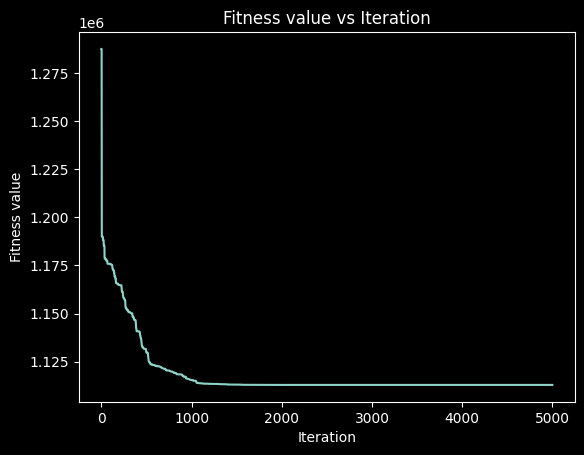
def Fplot(self):
# PLOTS GLOBAL FITNESS (OR COST) VALUE VS ITERATION GRAPH
plt.plot(self.time, self.fitness_time)
plt.title("Fitness value vs Iteration")
plt.xlabel("Iteration")
plt.ylabel("Fitness value")
plt.show()
################################################# END OF PSO CLASS ######################################################################
Fitness Function
def fitness_function(weights):
predictions = X @ weights[:-1] + weights[-1] # w1*X1 + w2*X2 + w3*X3 + w4*X4 + w5
error = np.sum((Y - predictions) ** 2) # MSE hesaplama. Çıkarma işlemi vektörler arasında yapılıyor.
return error
Create PSO Model
pso = PSO(
P=100, # parçacık sayısı
fitness=fitness_function, # uygunluk fonksiyonu
# X0=weights, # başlangıç değerleri. Eğer verilmezse rastgele değerler atanır.
n=5, # boyut sayısı
bound=[
(-100, 100),
(-100, 100),
(-100, 100),
(-100, 100),
(-100, 100),
], # arama uzayı sınırları
Tmax=5000, # maksimum iterasyon sayısı
verbose=True, # iterasyon bilgilerini yazdır
min=True, # uygunluk fonksiyonunu minimize et
plot=True, # uygunluk fonksiyonunun grafiğini çiz
)
Run PSO
pso.execute()
Iteration: 0 | best global fitness (cost): 1287415.9750612
Iteration: 1 | best global fitness (cost): 1287415.9750612
Iteration: 2 | best global fitness (cost): 1287415.9750612
Iteration: 3 | best global fitness (cost): 1190029.9669915
Iteration: 4 | best global fitness (cost): 1190029.9669915
Iteration: 5 | best global fitness (cost): 1190029.9669915
Iteration: 6 | best global fitness (cost): 1190029.9669915
Iteration: 7 | best global fitness (cost): 1190029.9669915
Iteration: 8 | best global fitness (cost): 1190029.9669915
...
...
...
Iteration: 4990 | best global fitness (cost): 1112990.1376006
Iteration: 4991 | best global fitness (cost): 1112990.1376006
Iteration: 4992 | best global fitness (cost): 1112990.1376006
Iteration: 4993 | best global fitness (cost): 1112990.1376006
Iteration: 4994 | best global fitness (cost): 1112990.1376006
Iteration: 4995 | best global fitness (cost): 1112990.1376006
Iteration: 4996 | best global fitness (cost): 1112990.1376006
Iteration: 4997 | best global fitness (cost): 1112990.1376006
Iteration: 4998 | best global fitness (cost): 1112990.1376006
Iteration: 4999 | best global fitness (cost): 1112990.1376006
Iteration: 5000 | best global fitness (cost): 1112990.1376006
OPTIMUM SOLUTION
> [-2e-07, 2e-07, -1.8e-06, 3.8e-06, 70.0972888]
OPTIMUM FITNESS
> 1112990.1376006