Naive Bayes
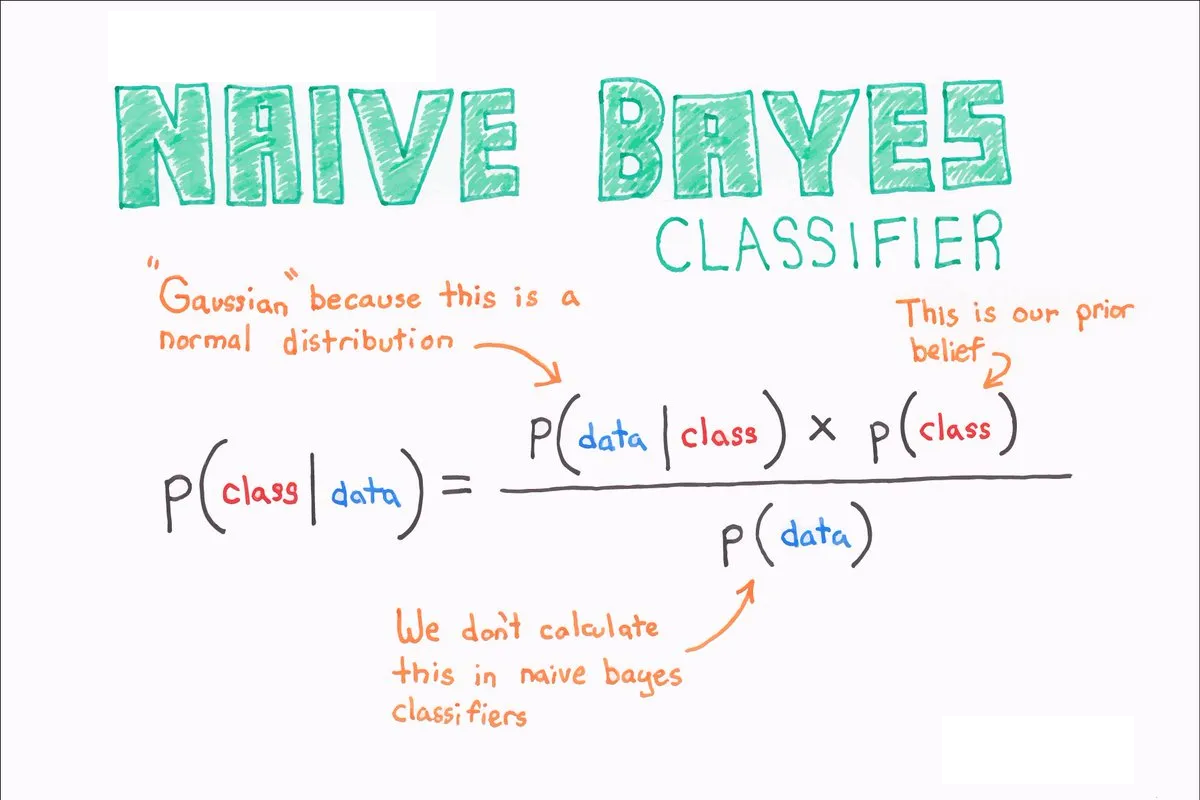
Naive Bayes algoritması, olasılık teorisine dayalı, basit ve hızlı bir makine öğrenme algoritmasıdır. Özellikle sınıflandırma problemlerinde sıkça kullanılır. Algoritmanın temel prensibi, Bayes Teoremi’ne dayanarak sınıf olasılıklarını tahmin etmektir.
Naive Bayes, bağımsızlık varsayımı (naive assumption) yapar; yani bir veri kümesindeki özelliklerin birbirinden bağımsız olduğunu kabul eder. Bu, gerçek dünyada nadiren doğru olsa da, birçok problemde etkili sonuçlar verir.
Naive Bayes, adını iki temel varsayımdan alır:
1. Bayes Teoremi
Naive Bayes algoritması Bayes Teoremi’ni temel alır. Bayes Teoremi, bir olayın olasılığını, o olaya ait gözlemlere ve diğer ilgili olayların olasılıklarına dayanarak hesaplamamıza olanak tanır. Formülü şu şekildedir: \[P(C|X) = \frac{P(X|C) * P(C)}{P(X)}\]
- \(P(C\|X)\) : \(X\) olayının gerçekleştiği bilindiğinde \(C\) olayının gerçekleşme olasılığıdır. Yani \(X\) verisinin sınıfı \(C\) olma olasılığıdır.
- \(P(X\|C)\) : \(C\) olayının gerçekleştiği bilindiğinde \(X\) olayının gerçekleşme olasılığıdır. Yani sınıf \(C\) verildiğinde \(X\) verisinin gözlenme olasılığıdır.
- \(P(C)\) : Sınıf \(C\) olasılığı.
- \(P(X)\) : \(X\) verisinin gözlenme olasılığı.
2. Naive Varsayım (Bağımsızlık Varsayımı):
Naive Bayes’in en önemli varsayımı, tüm özelliklerin (feature) birbirinden bağımsız olduğudur. Yani bir özelliğin değeri, diğer özelliklerin değeriyle bağımsızdır. Bu varsayım genellikle gerçek dünyada nadiren geçerlidir, ancak yine de çoğu durumda algoritmanın iyi performans göstermesine engel olmaz.
Naive Bayes Algoritması Türleri
Naive Bayes algoritmasının birkaç çeşidi vardır ve farklı veri dağılımlarına göre uygulanır:
Gaussian Naive Bayes
Özellikler sürekli olduğunda ve normal dağılıma uygun olduğunda kullanılır.
Multinomial Naive Bayes
Belirli sayıda kategoriye sahip veriler için kullanılır. Özellikle metin sınıflandırma problemlerinde yaygın olarak kullanılır. Kelime sayımı gibi verilerle çalışır.
Bernoulli Naive Bayes
İkili (binary) veriler için uygundur.
Avantajları
- Hızlı ve Verimli: Hesaplama açısından çok hızlıdır ve büyük veri setleriyle bile iyi ölçeklenir.
- Az Veriyle İyi Sonuçlar: Özellikle veri seti küçükken dahi iyi sonuçlar verebilir.
- Kolay Uygulama: Scikit-learn gibi kütüphaneler sayesinde kolayca uygulanabilir.
- Yüksek boyutlu verilerle iyi başa çıkar.
Dezavantajları
- Bağımsızlık Varsayımı: Özelliklerin birbirinden bağımsız olması varsayımı gerçek dünyada genellikle geçerli olmadığından bazen yanıltıcı olabilir.
- Sürekli Veriler İçin Zayıflık: Gaussian Naive Bayes dışında, genellikle sürekli verilerle çalışmada zayıf performans gösterebilir.
Sample App
Şimdi Naive Bayes algoritması ile sınıflandırma yaparak diabet hastalığını tahmin eden bir model geliştirelim.
Dataset
About Dataset
Bu veriseti 768 gözlem ve 8 sayısal bağımsız değişkenden oluşmaktadır.
Bağımlu ve hedef değişken OUTCOME (sonuç)’dur.
- 1 diabet testi sonucunun pozitif,
0 ise diabet testi sonucunun negtif olduğunu gösterir.
- Pregnancies: Hastanın kaç kere hamile kaldığını gösterir.
- Glucose: 2 saatlik oral glukoz tolerans testinde plazma glukoz konsantrasyonu.
- BloodPressure: Diastolic kan basıncı (mm Hg)
- SkinThickness: Triceps cilt kıvrımı kalınlığı (mm).
- Insulin: 2 saatlik serum insülin düzeyi (mu U/ml).
- BMI: Vücut kitle indeksi (ağırlık kg / boy m²).
- DiabetesPedigreeFunction: Aile geçmişine dayalı olarak diyabet olasılığını hesaplayan bir fonksiyon.
- Age: Hastanın yaşı.
- Outcome: Diyabet durumu (0 = diyabet yok, 1 = diyabet var).
Import the necessary modules and libraries
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
# Models
from sklearn.naive_bayes import GaussianNB
#Performance metrices
from sklearn.metrics import confusion_matrix, accuracy_score,classification_report
#For ignoring warnings
import warnings
warnings.filterwarnings("ignore")
Load the Data
data = pd.read_csv('diabetes.csv')
print(data.head())
Pregnancies Glucose BloodPressure SkinThickness Insulin BMI \
0 6 148 72 35 0 33.6
1 1 85 66 29 0 26.6
2 8 183 64 0 0 23.3
3 1 89 66 23 94 28.1
4 0 137 40 35 168 43.1
DiabetesPedigreeFunction Age Outcome
0 0.627 50 1
1 0.351 31 0
2 0.672 32 1
3 0.167 21 0
4 2.288 33 1
checking the number of rows and columns
print(data.shape)
(768, 9)
# getting the some information about the data
print(data.info())
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 768 entries, 0 to 767
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Pregnancies 768 non-null int64
1 Glucose 768 non-null int64
2 BloodPressure 768 non-null int64
3 SkinThickness 768 non-null int64
4 Insulin 768 non-null int64
5 BMI 768 non-null float64
6 DiabetesPedigreeFunction 768 non-null float64
7 Age 768 non-null int64
8 Outcome 768 non-null int64
dtypes: float64(2), int64(7)
memory usage: 54.1 KB
None
# checking for the missing values
print(data.isnull().sum())
Pregnancies 0
Glucose 0
BloodPressure 0
SkinThickness 0
Insulin 0
BMI 0
DiabetesPedigreeFunction 0
Age 0
Outcome 0
dtype: int64
# Check number of unique values in each column
for i in data.columns:
print(i, len(data[i].unique()))
Pregnancies 17
Glucose 136
BloodPressure 47
SkinThickness 51
Insulin 186
BMI 248
DiabetesPedigreeFunction 517
Age 52
Outcome 2
# Descriptive statistics
print(data.describe())
Pregnancies Glucose BloodPressure SkinThickness Insulin \
count 768.000000 768.000000 768.000000 768.000000 768.000000
mean 3.845052 120.894531 69.105469 20.536458 79.799479
std 3.369578 31.972618 19.355807 15.952218 115.244002
min 0.000000 0.000000 0.000000 0.000000 0.000000
25% 1.000000 99.000000 62.000000 0.000000 0.000000
50% 3.000000 117.000000 72.000000 23.000000 30.500000
75% 6.000000 140.250000 80.000000 32.000000 127.250000
max 17.000000 199.000000 122.000000 99.000000 846.000000
BMI DiabetesPedigreeFunction Age Outcome
count 768.000000 768.000000 768.000000 768.000000
mean 31.992578 0.471876 33.240885 0.348958
std 7.884160 0.331329 11.760232 0.476951
min 0.000000 0.078000 21.000000 0.000000
25% 27.300000 0.243750 24.000000 0.000000
50% 32.000000 0.372500 29.000000 0.000000
75% 36.600000 0.626250 41.000000 1.000000
max 67.100000 2.420000 81.000000 1.000000
# Check the distribution of the target variable
print(data['Outcome'].value_counts())
Outcome
0 500
1 268
Name: count, dtype: int64
Graphical Analysis of Data
# correlation matrix
corr = data.corr()
plt.figure(figsize=(20,10))
sns.heatmap(corr, annot=True, cmap='BuPu')
plt.show()
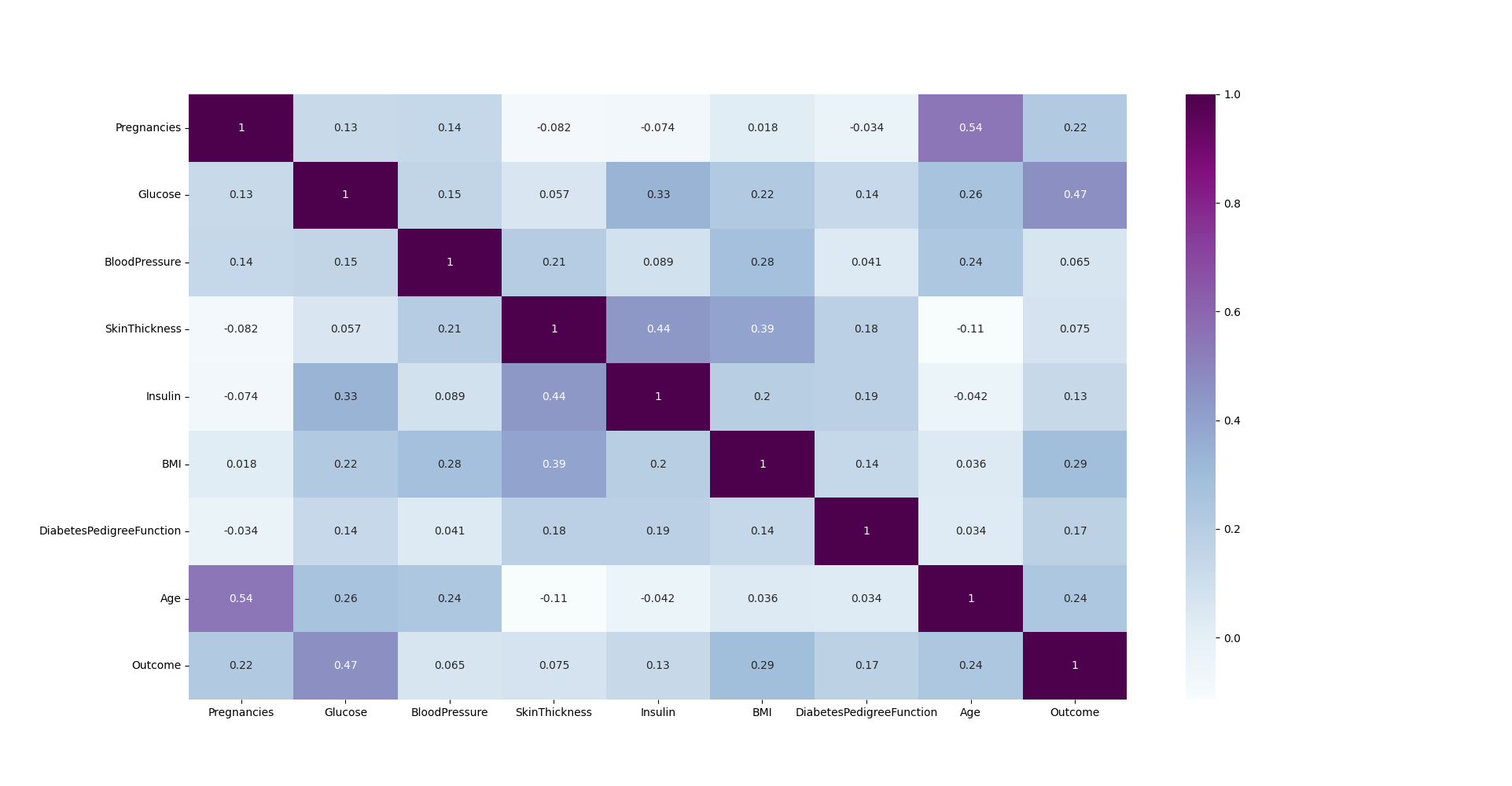
Korelasyon ısı haritasına göre;
- Glukoz ve Outcome (diyabet durumu) arasında pozitif bir korelasyon bulunuyor, yani yüksek glukoz seviyeleri diyabetle daha çok ilişkili.
- BMI ve Outcome arasında da bir ilişki mevcut, ancak daha zayıf.
- Pregnancies ve outcome arasındada zayıf bir ilişki var ancak bu sütunu çıkartıyorum.
data.drop('Pregnancies', axis=1, inplace=True)
plt.figure(figsize=(8,8))
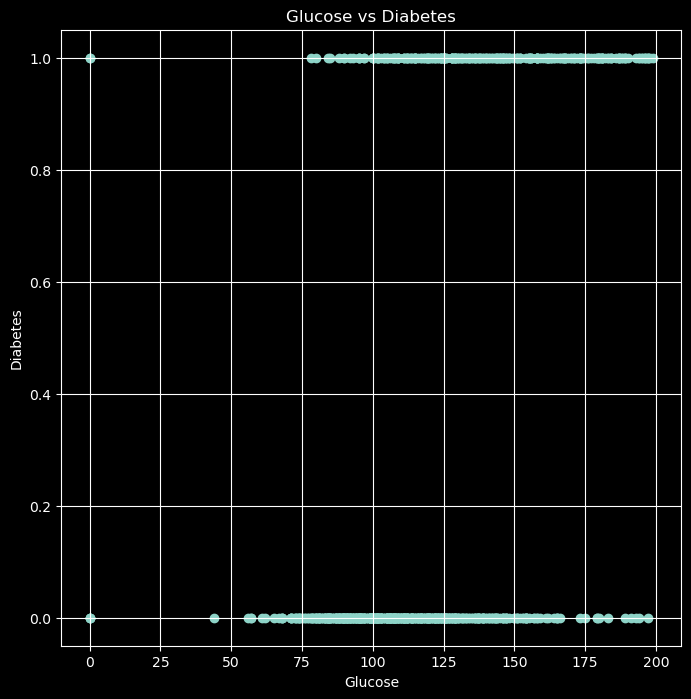
plt.scatter(data['Glucose'],data['Outcome'])
plt.xlabel('Glucose')
plt.ylabel('Diabetes')
plt.title('Glucose vs Diabetes')
plt.grid()
plt.figure(figsize=(8,8))
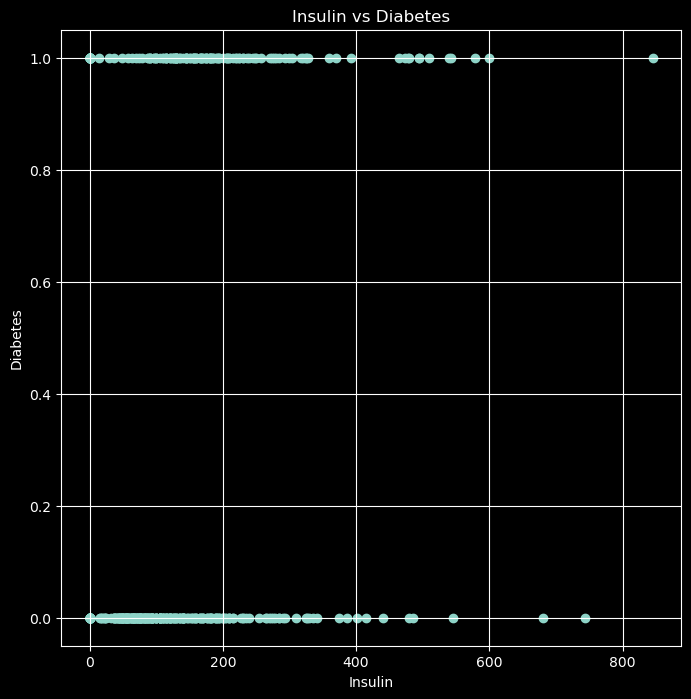
plt.scatter(data['Insulin'],data['Outcome'])
plt.xlabel('Insulin')
plt.ylabel('Diabetes')
plt.title('Insulin vs Diabetes')
plt.grid()
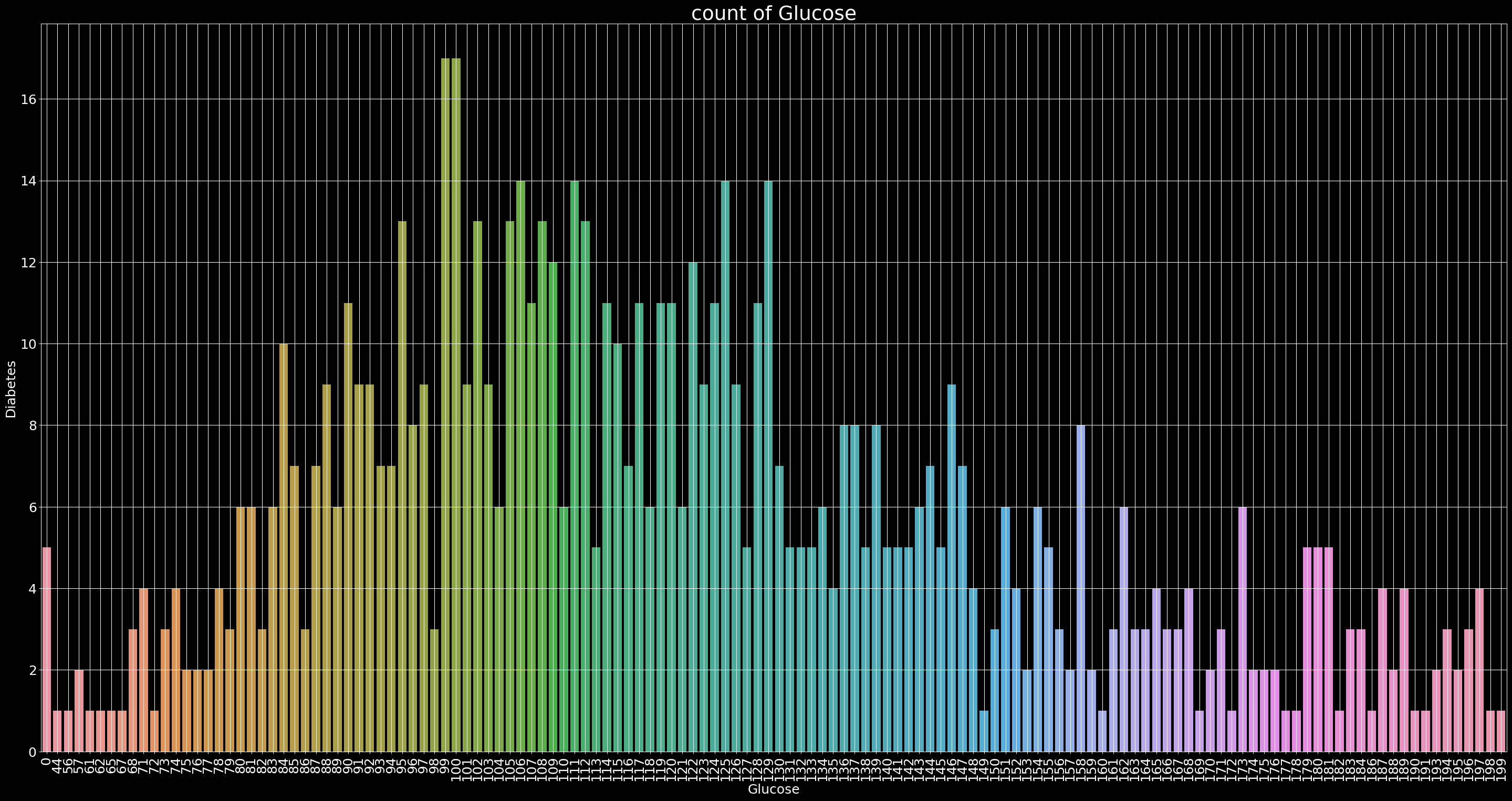
Count of Glucose
plt.figure(figsize=(40,20),dpi=90)
ax=sns.countplot(x='Glucose',data=data)
plt.xticks(rotation=90, fontsize=20)
plt.yticks(fontsize=20)
plt.xlabel('Glucose',fontsize=20)
plt.ylabel('Diabetes',fontsize=20)
plt.title('count of Glucose',fontsize=30)
plt.grid()
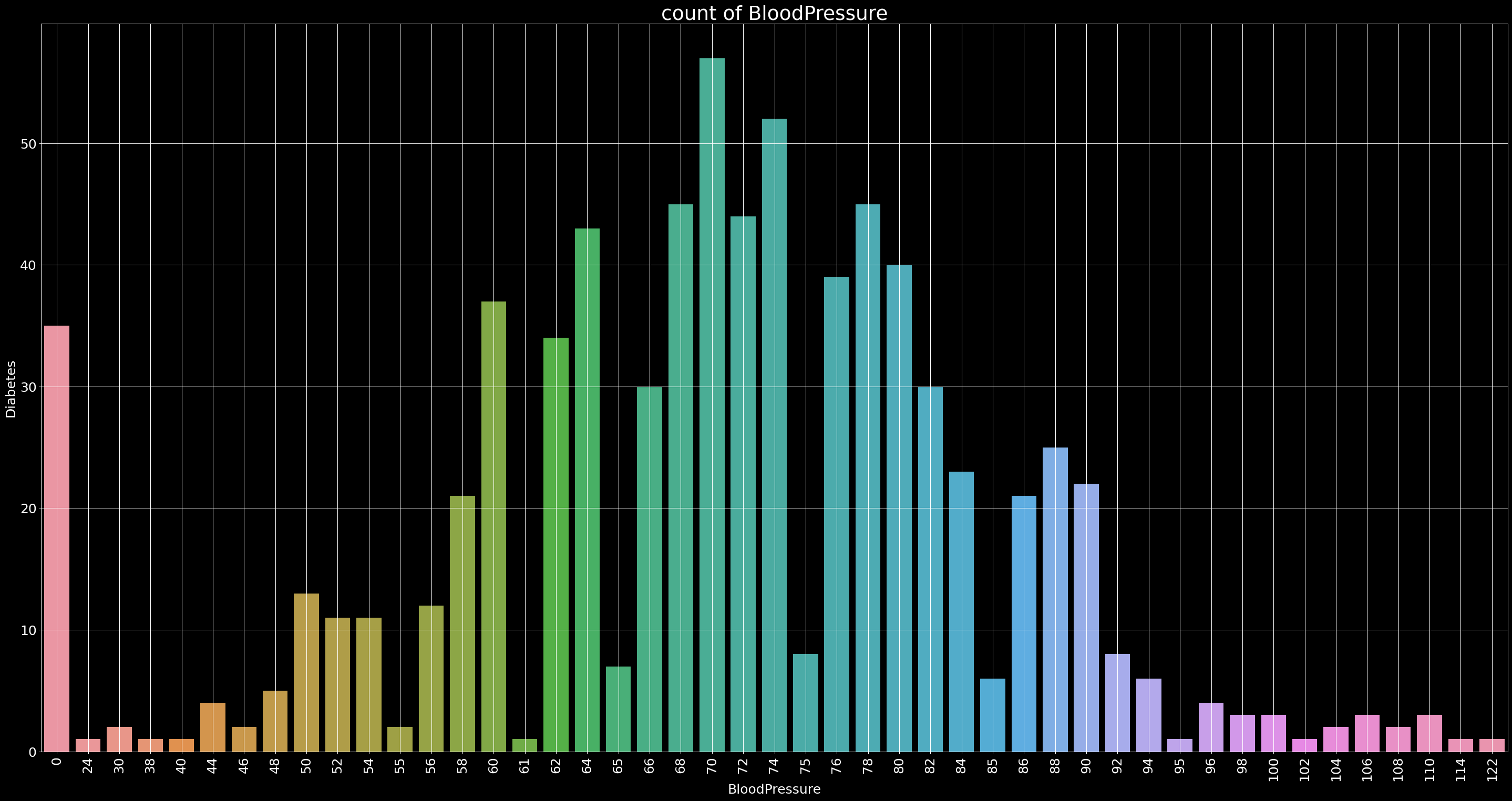
Count of BloodPressure
plt.figure(figsize=(40,20),dpi=90)
ax=sns.countplot(x='BloodPressure',data=data)
plt.xticks(rotation=90, fontsize=20)
plt.yticks(fontsize=20)
plt.xlabel('BloodPressure',fontsize=20)
plt.ylabel('Diabetes',fontsize=20)
plt.title('count of BloodPressure',fontsize=30)
plt.grid()
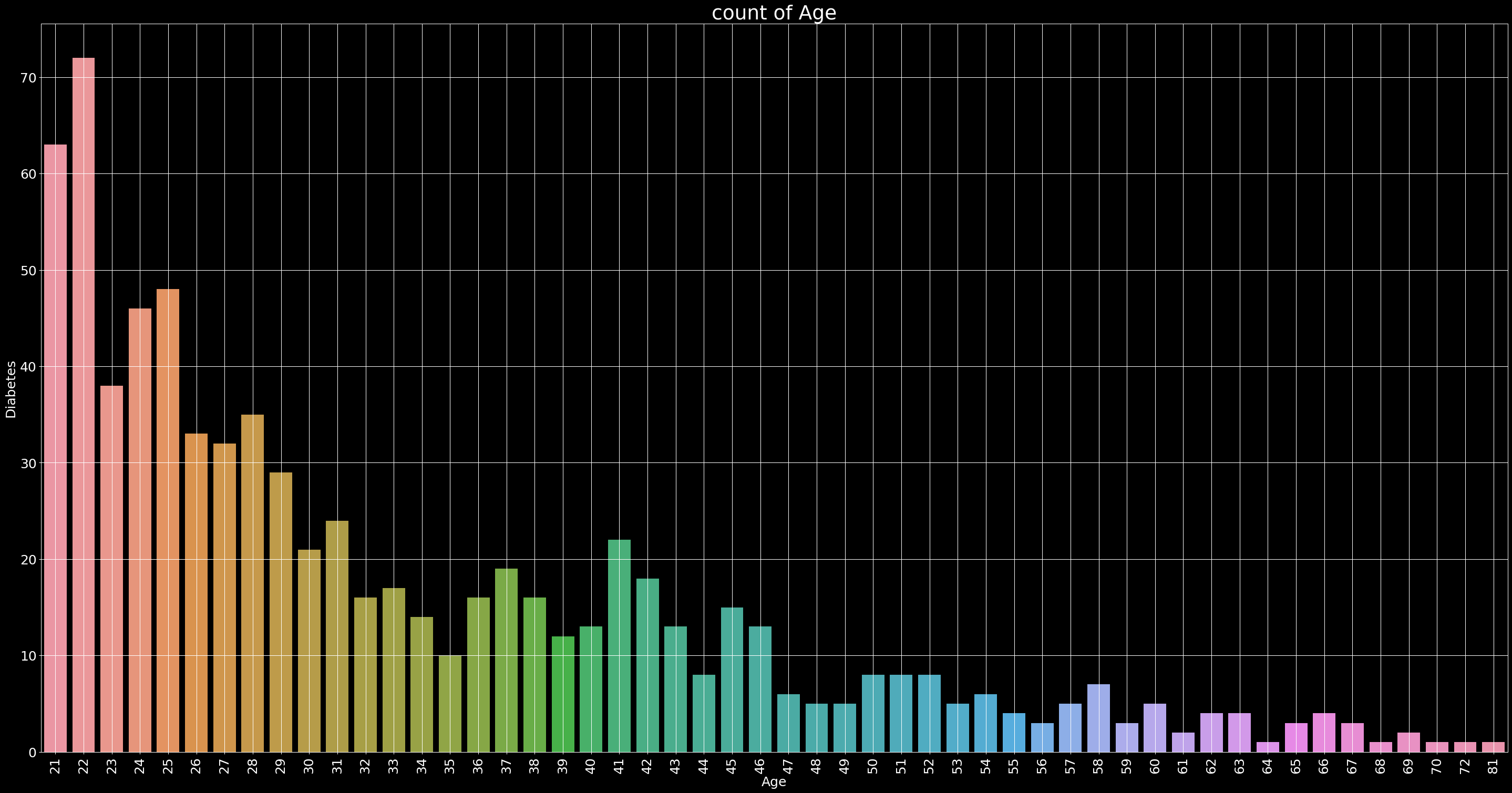
Count of Age
plt.figure(figsize=(40,20),dpi=90)
ax=sns.countplot(x='Age',data=data)
plt.xticks(rotation=90, fontsize=20)
plt.yticks(fontsize=20)
plt.xlabel('Age',fontsize=20)
plt.ylabel('Diabetes',fontsize=20)
plt.title('count of Age',fontsize=30)
plt.grid()
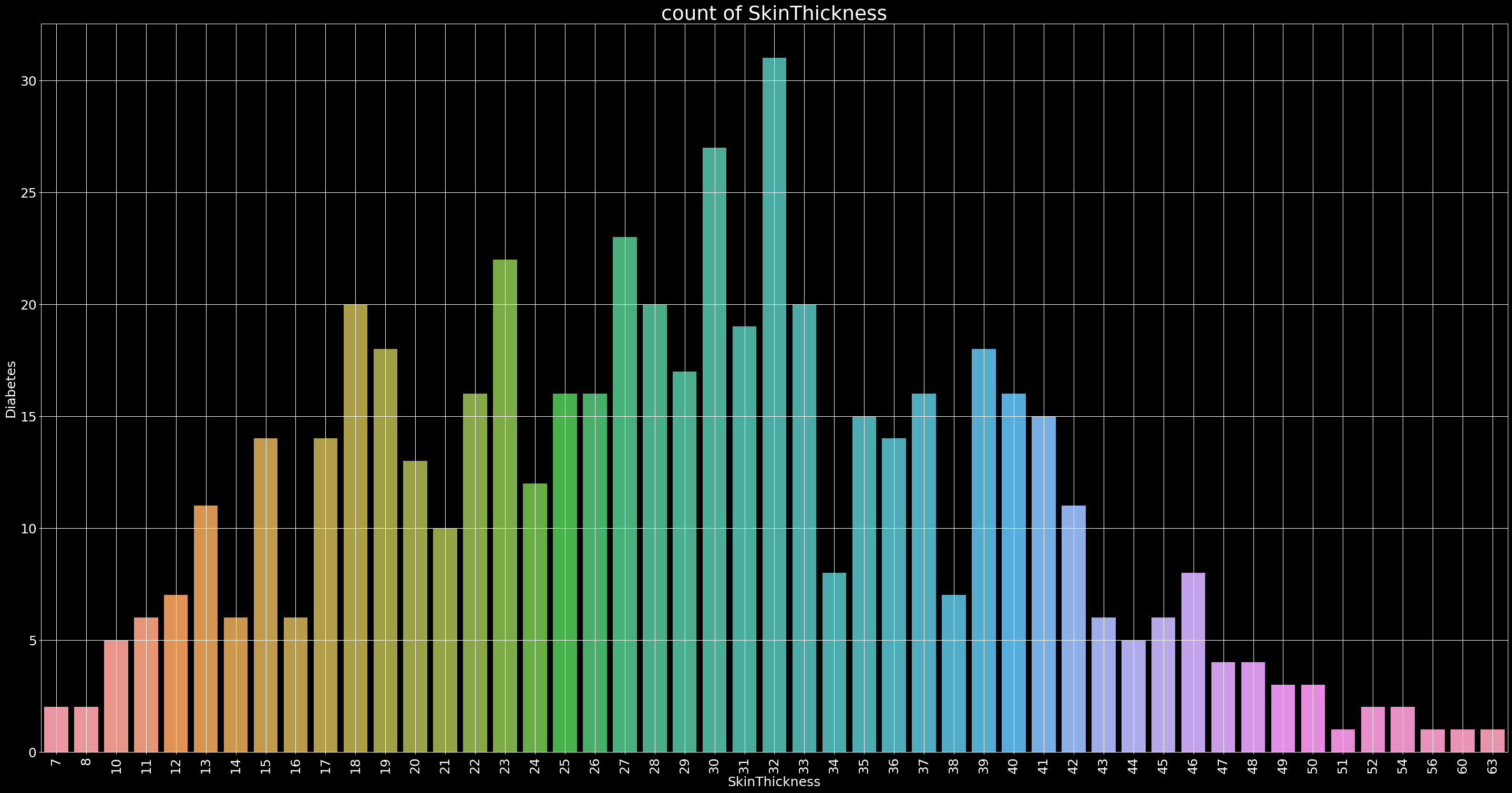
Count of SkinThickness
plt.figure(figsize=(40,20),dpi=90)
ax=sns.countplot(x='SkinThickness',data=data)
plt.xticks(rotation=90, fontsize=20)
plt.yticks(fontsize=20)
plt.xlabel('SkinThickness',fontsize=20)
plt.ylabel('Diabetes',fontsize=20)
plt.title('count of SkinThickness',fontsize=30)
plt.grid()
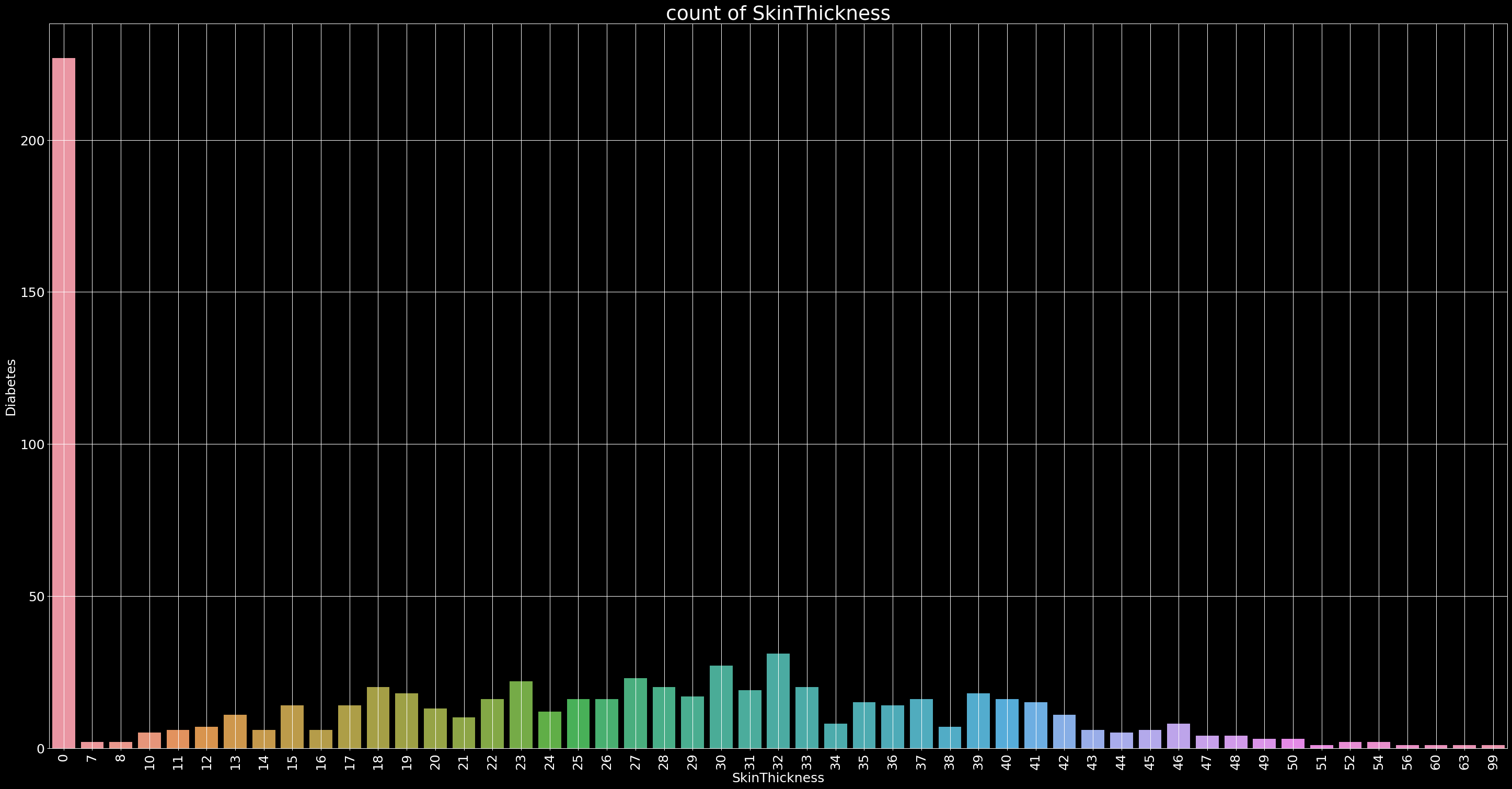
Grafikdende anlaşılacağı üzere cilt kalınlığı 0 olan aykırı değerleri çıkartıyorum.
# drop the outliers
data=data[data['SkinThickness']>0]
data=data[data['SkinThickness']<90]
plt.figure(figsize=(40,20),dpi=90)
ax=sns.countplot(x='SkinThickness',data=data)
plt.xticks(rotation=90, fontsize=20)
plt.yticks(fontsize=20)
plt.xlabel('SkinThickness',fontsize=20)
plt.ylabel('Diabetes',fontsize=20)
plt.title('count of SkinThickness',fontsize=30)
plt.grid()
data.dropna(how='any', inplace=True) # drop the missing values
data.reset_index(drop=True, inplace=True) # reset the index
# last shape of the data
print(data.shape)
(540, 8)
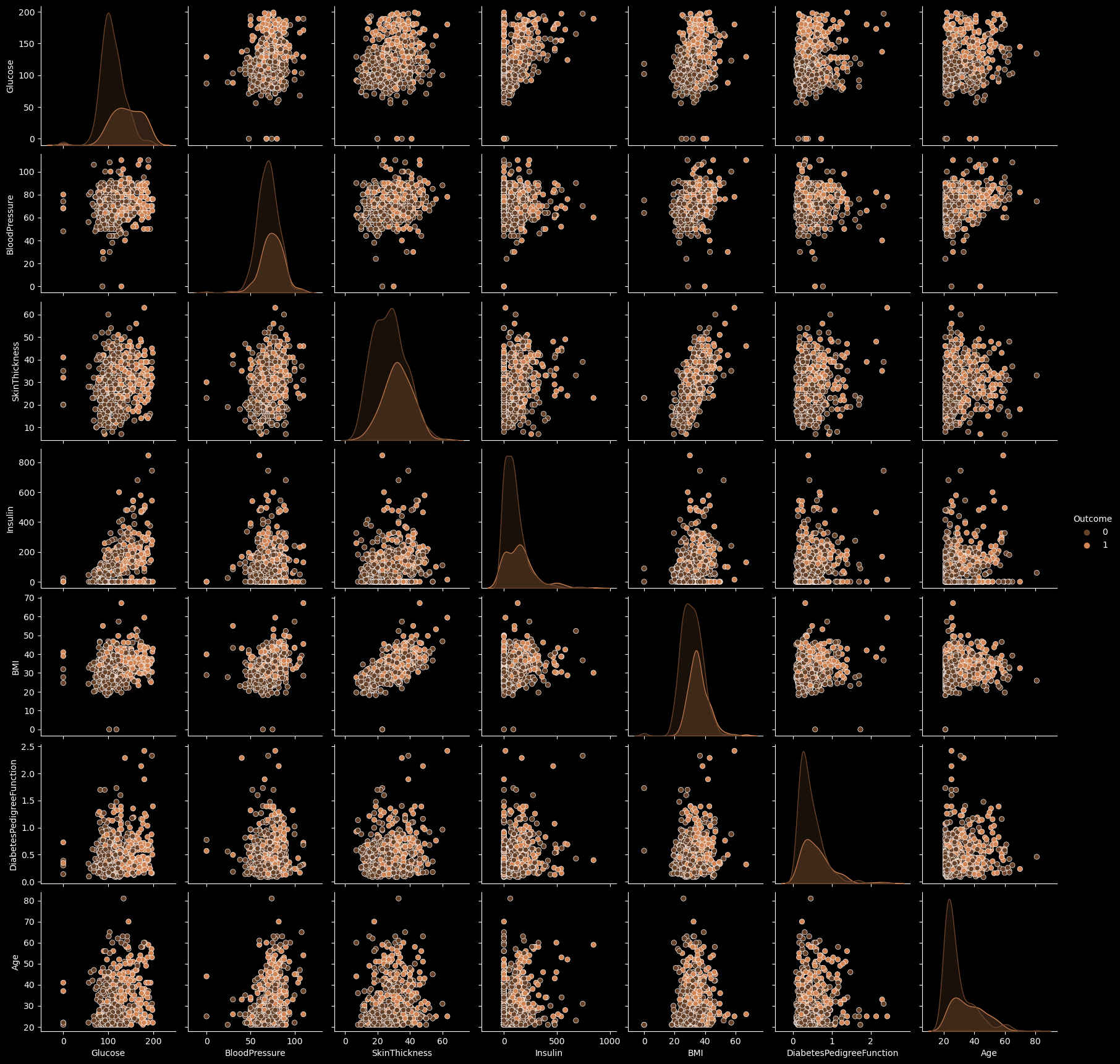
pairplot
sns.pairplot(data=data, diag_kind='kde', hue='Outcome',palette='copper')
plt.show()
Normalization
scaler = MinMaxScaler()
data_scaled = scaler.fit_transform(data)
data_scaled = pd.DataFrame(data_scaled, columns=data.columns)
Separating the independent and dependent variables
x = data_scaled.drop('Outcome', axis=1)
y = data_scaled['Outcome']
Splitting the data
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.35, random_state=0)
Create a Gaussian Classifier
model = GaussianNB()
model.fit(x_train, y_train)
GaussianNB()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
GaussianNB()
Prediction
# Predict the response for test dataset
y_pred = model.predict(x_test)
Model Accuracy
print("Accuracy:", accuracy_score(y_test, y_pred))
Accuracy: 0.7671957671957672
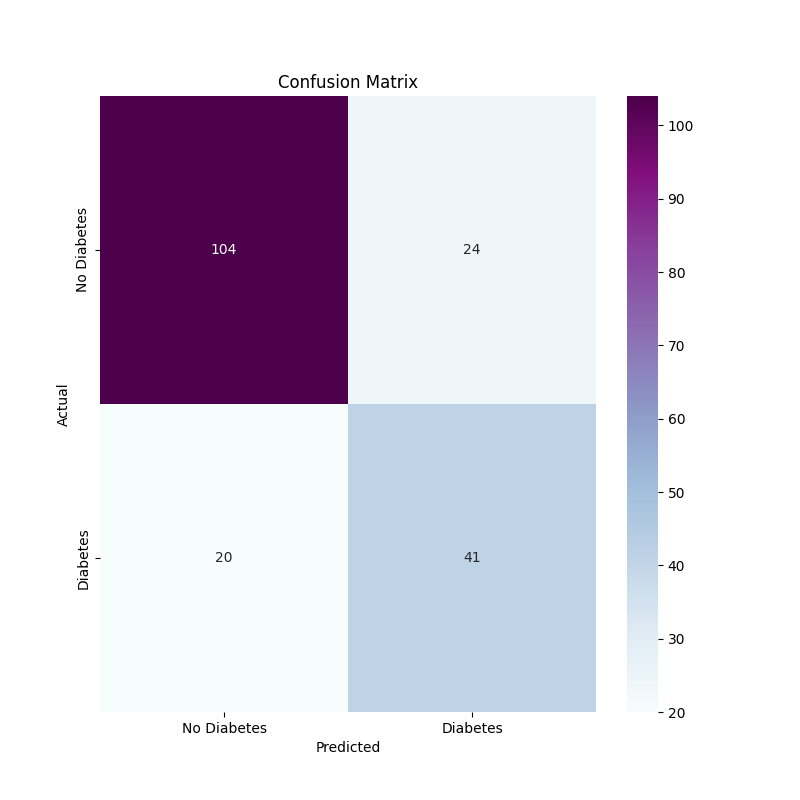
confusion matrix
cm = confusion_matrix(y_test, y_pred)
plt.figure(figsize=(8,8))
sns.heatmap(cm, annot=True, fmt='d', cmap='BuPu', xticklabels=['No Diabetes', 'Diabetes'], yticklabels=['No Diabetes', 'Diabetes'])
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.title('Confusion Matrix')
plt.show()
classification report
print(classification_report(y_test, y_pred))
precision recall f1-score support
0.0 0.84 0.81 0.83 128
1.0 0.63 0.67 0.65 61
accuracy 0.77 189
macro avg 0.73 0.74 0.74 189
weighted avg 0.77 0.77 0.77 189
Example patient
patient = [[0.6, 0.8, 0.56, 0.4, 0.5, 0.6, 0.7]]
# Making prediction
pred = model.predict(patient)
if pred[0] == 0:
print('The patient is not diabetic')
else:
print('The patient is diabetic')
The patient is diabetic
0.77 accuracy değerine sahip kabul edilebilir ölçüde bir model oluşturduk.
Son olarak örnek hastanın değerleri verildğinde, modelimiz bu hastanın diabet hastası olduğunu öngördü.