Support Vector Machine (SVM)

Categorized under Machine Learning tagged Classification Last modified at:
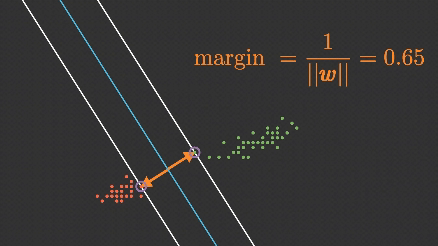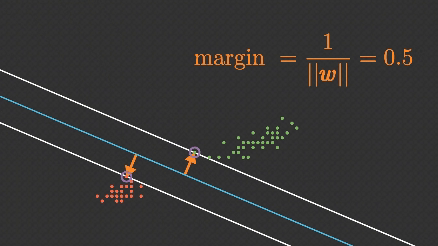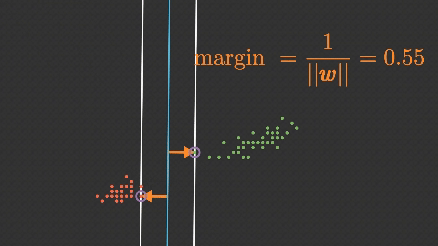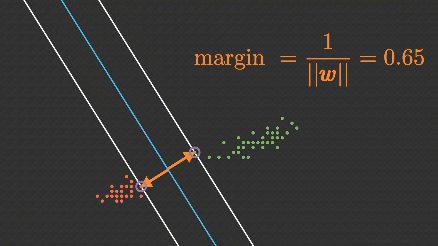
Support Vector Machine (SVM)

Support Vector Machine (SVM) algoritması, makine öğrenmesinde hem sınıflandırma hem de regresyon problemlerinde yaygın olarak kullanılan, özellikle küçük ve orta boyutlu veri setlerinde etkili olan güçlü bir algoritmadır.

SVM, genellikle doğrusal olarak ayrılabilir verilerde kullanılsa da, doğrusal olmayan verilerde de çalışabilmek için kernel yöntemleriyle genişletilebilir.

Support Vector Machine Algoritmasının Temel Kavramları

Support Vector Machine

1. Hyperplane (Hiperdüzlem)

SVM’in amacı, verileri ayıran en iyi hiperdüzlemi bulmaktır. Hiperdüzlem, veriyi sınıflara ayıran bir sınır çizgisi olarak düşünülebilir. İki boyutlu uzayda bir doğru, üç boyutlu uzayda bir düzlem ve daha yüksek boyutlarda da bir hiperdüzlem ile temsil edilir.

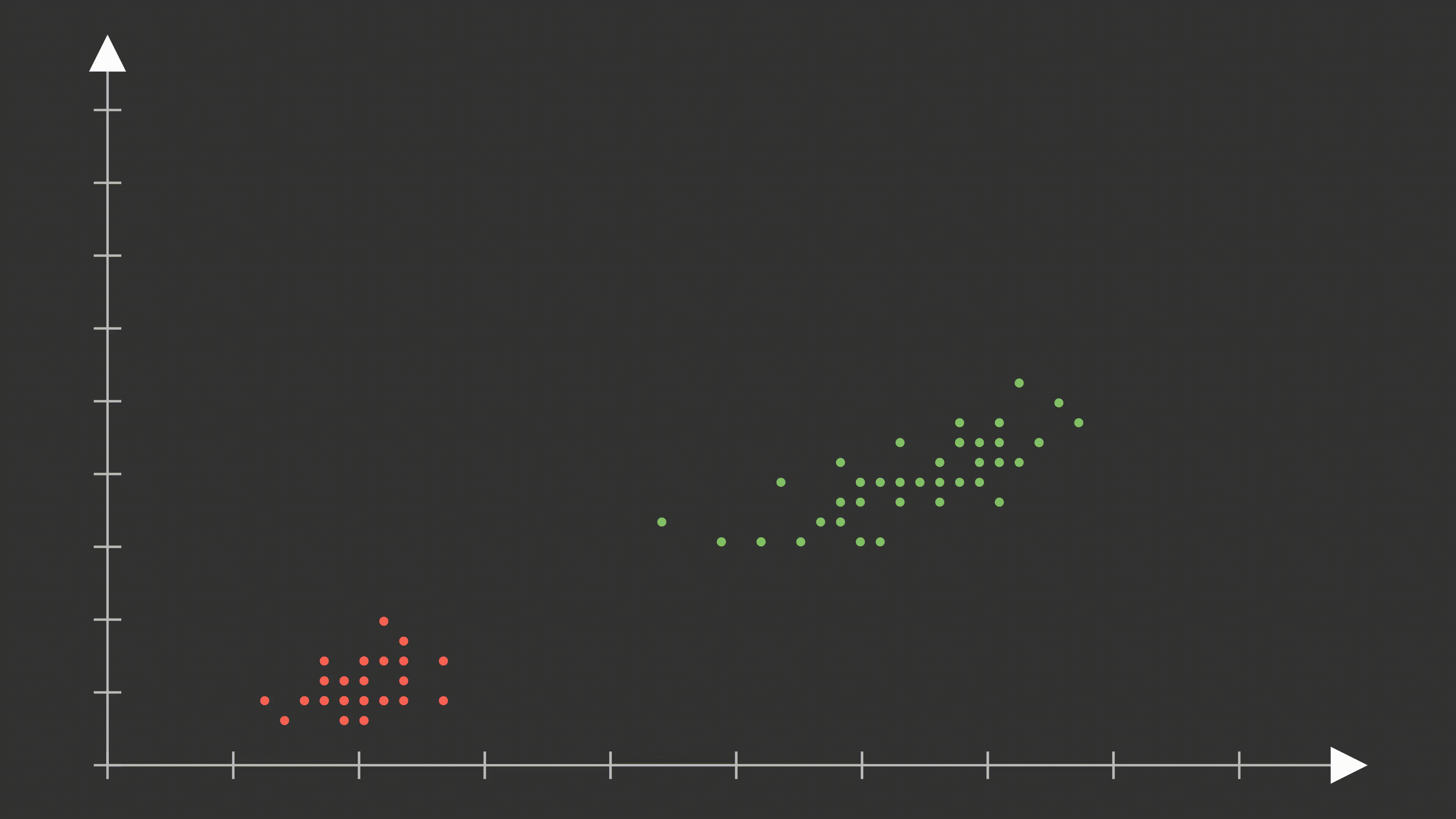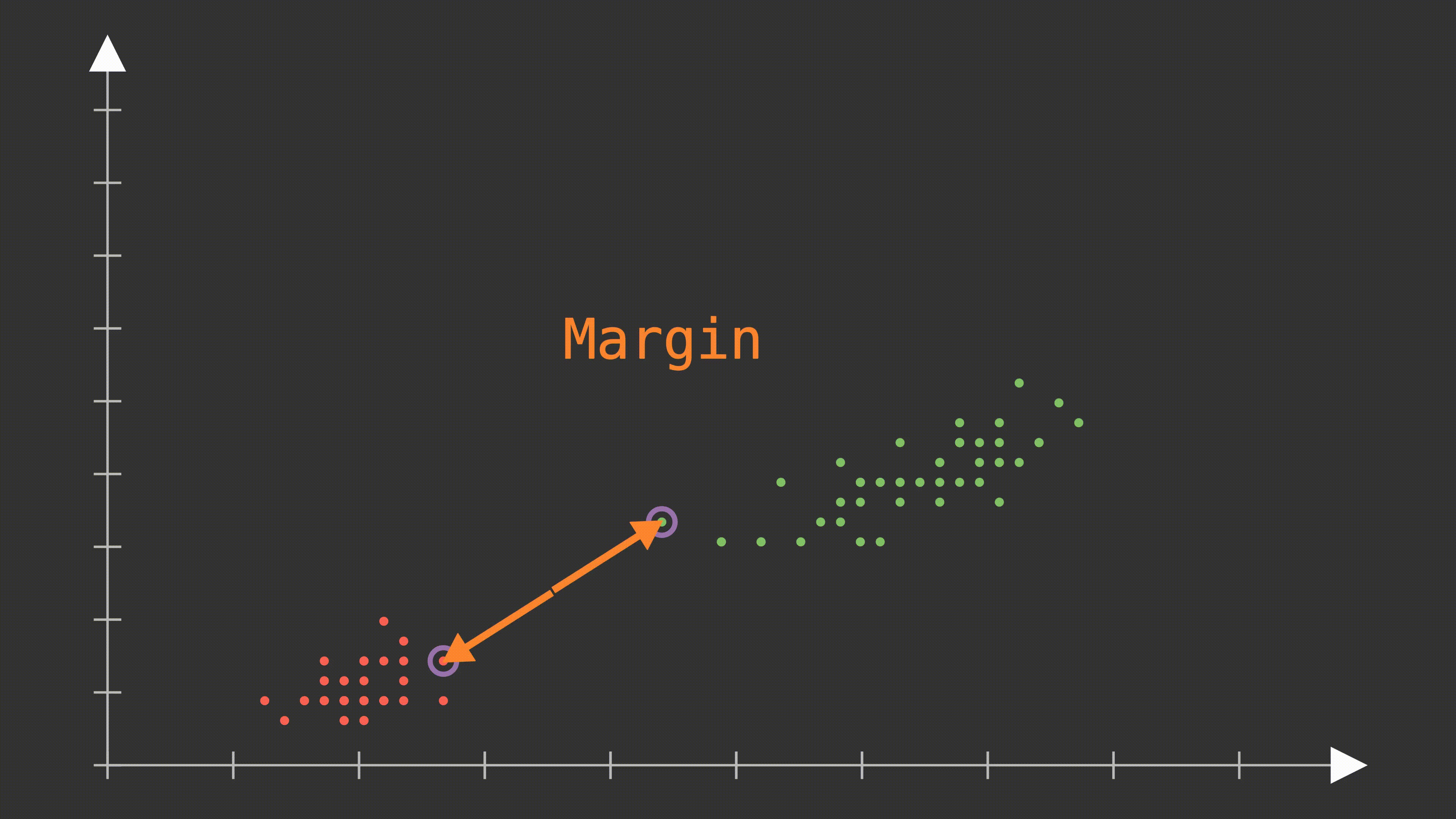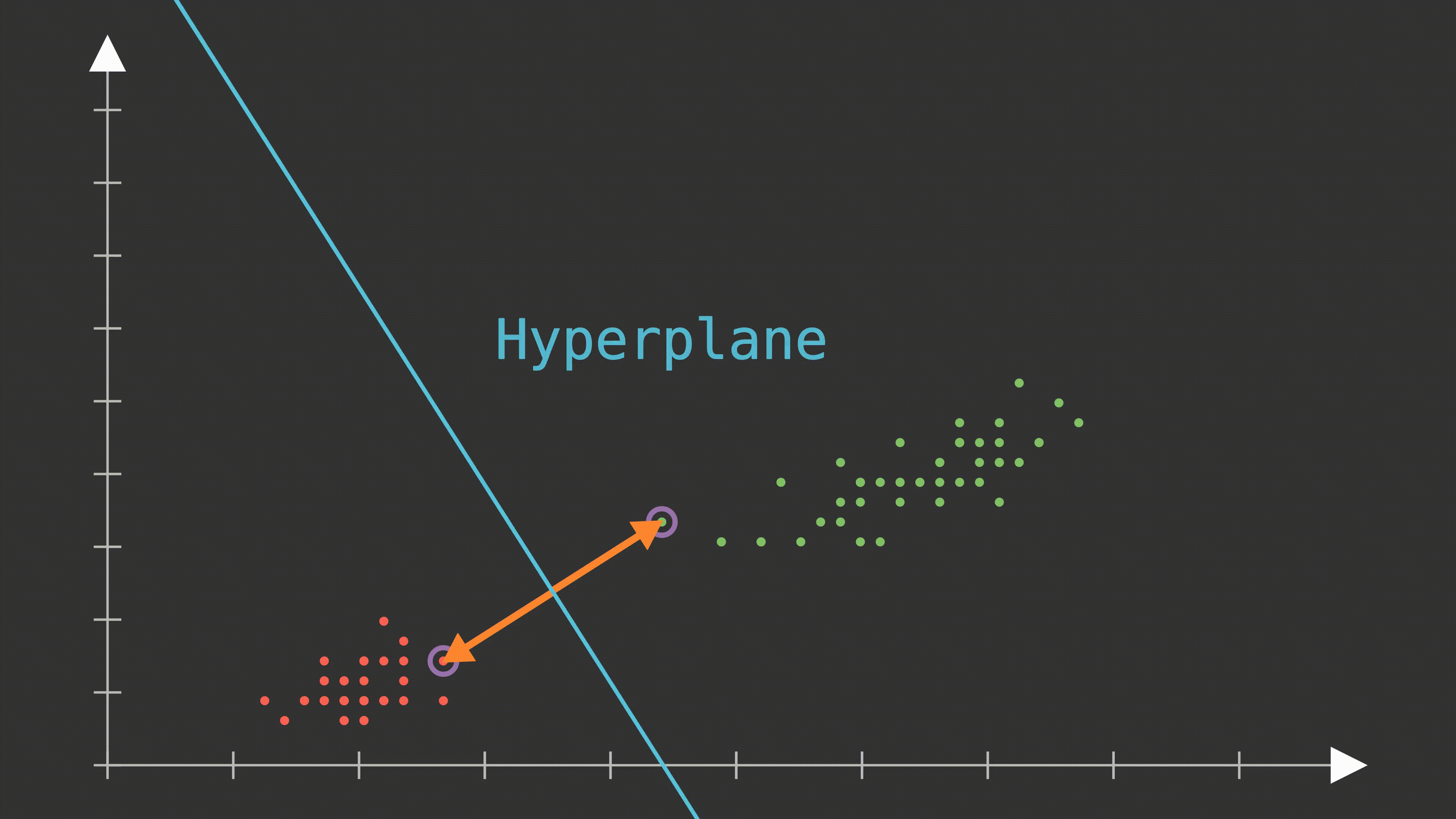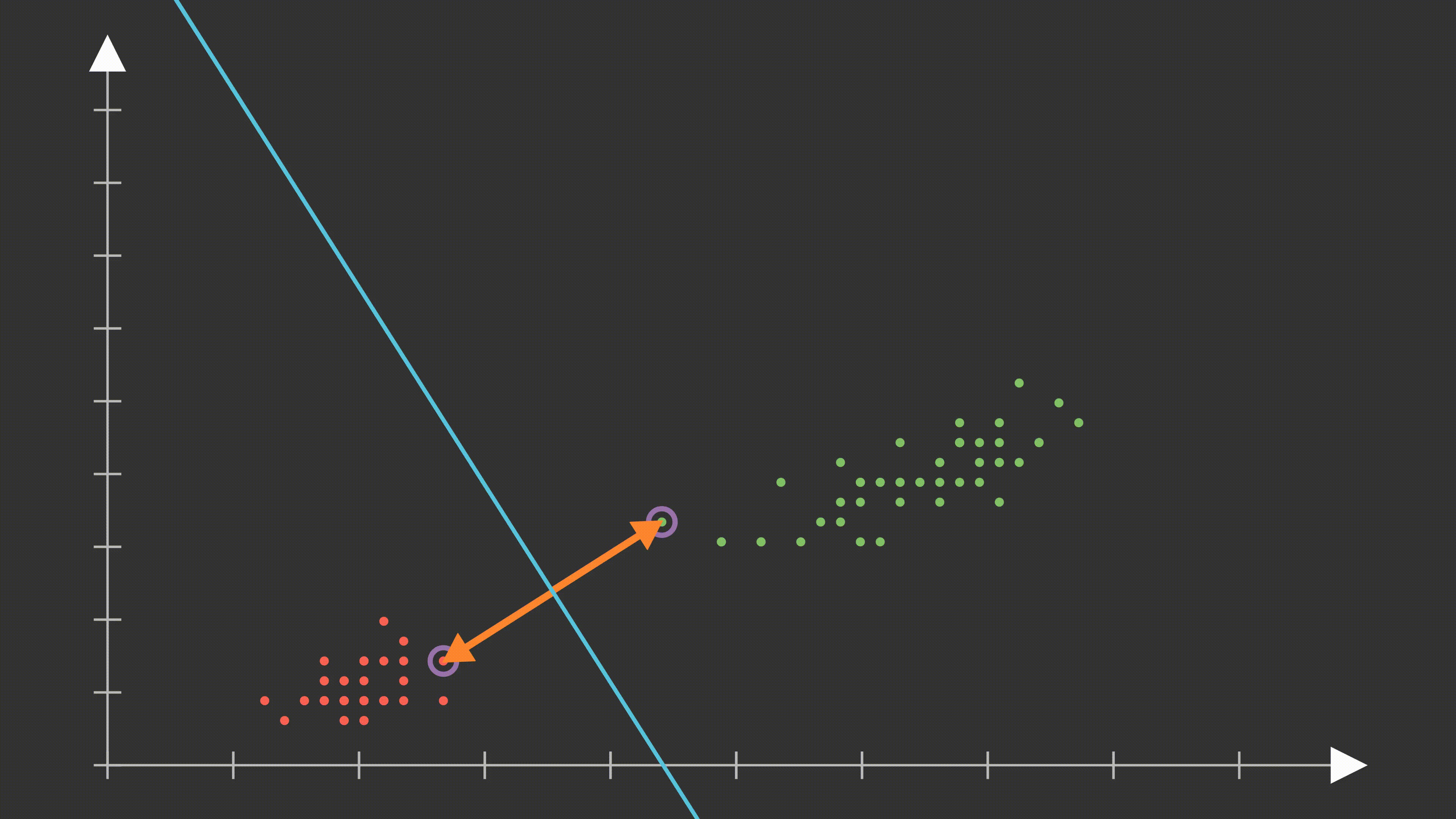
2. Margin (Marjin)

Hiperdüzlemden her iki sınıfa en yakın veriler arasındaki mesafeye marjin denir. SVM, bu marjini maksimum yapmak ister. Marjini maksimize etmek, modelin doğruluk ve genelleme yeteneğini artırır.

3. Support Vectors (Destek Vektörleri)

Sınıfları ayıran hiperdüzleme en yakın veri noktalarına support vectors denir. Hiperdüzlem, bu destek vektörlerine dayanarak belirlenir. Geri kalan veri noktaları hiperdüzlemi etkilemez.

Doğrusal Olarak Ayrılabilir Veriler

Doğrusal olarak ayrılabilir verilerde, SVM iki sınıfı ayırmak için en geniş marjini bulmaya çalışır. Hiperdüzlem seçimi, şu koşulları sağlar:

  • İki sınıfa ait veri noktalarından en uzak olanı seçilir.
  • Bu en uzak noktalar arasındaki marjin maksimum yapılır.

Amaç, sınıfları doğru bir şekilde ayıracak ve genelleme yapacak bir hiperdüzlem bulmaktır. Bu işlem, aşağıdaki optimizasyon problemiyle çözülür: \[min_{w,b}\frac{1}{2}\left|w\right|^2\]

Bu optimizasyon probleminde, 𝑤 hiperdüzlemi tanımlayan ağırlık vektörünü, 𝑏 ise bias terimini ifade eder. Amaç, ağırlıkları minimize ederken, hiperdüzlemin marjinini maksimum yapmaktır.

Doğrusal Olarak Ayrılamayan Veriler ve Kernel Fonksiyonları

Veri seti doğrusal olarak ayrılamıyorsa, veriyi daha yüksek boyutlu bir uzaya projelendirerek doğrusal hale getirmek için kernel trick denilen yöntem kullanılır. Kernel fonksiyonları, veri noktalarının daha yüksek boyutlu bir uzaya taşınmasını sağlar. Böylece veriler doğrusal olarak ayrılabilir hale gelir.

Yaygın Kernel Fonksiyonları

Linear Kernel

Doğrusal olarak ayrılabilen veriler için uygundur. \[K(x_i, x_j) = x_{i}^{T}x_{j}\]

Polynomial Kernel

Doğrusal olmayan ayrımlar için uygundur. Polinom derecesine göre şekillenir. \[K(x_i, x_j) = (x_{i}^{T}x_{j}+c)^d\]

Radial Basis Function (RBF) Kernel

Genellikle en yaygın kullanılan kernel fonksiyonudur ve çok karmaşık sınırları modelleyebilir. \[K(x_i, x_j) = exp(-γ\left|x_i-x_j\right|^2)\]

Sigmoid Kernel

Yapay sinir ağlarındaki aktivasyon fonksiyonuna benzeyen bir kernel fonksiyonudur. \[K(x_i, x_j) = tanh(αx_{i}^{T}x_j +c)\]

Scaling

Support Vector Machine (SVM) ile çalışırken scaling (ölçeklendirme) işlemi yapılması gereklidir. Bunun başlıca nedenleri:

1. SVR’nin Çekirdek Fonksiyonları ile Uyum

Çoğu SVR modeli, RBF (Radial Basis Function) ve polynomial gibi çekirdek fonksiyonları kullanır. Bu çekirdek fonksiyonları, özellikler arasındaki mesafelere dayalı olarak çalışır. Eğer özellikler farklı ölçeklerdeyse (örneğin biri 0-1 arasında, diğeri 1-1000 arasında), bu durum SVR’nin performansını olumsuz etkileyebilir çünkü daha büyük ölçekli özellikler modelde daha fazla ağırlık kazanır.

2. Optimizasyonun Daha Kolay Yapılması

SVR, optimizasyon sürecinde C (regülarizasyon parametresi) ve γ (gamma) gibi hiperparametreleri kullanır. Özelliklerin ölçeklenmesi bu hiperparametrelerin daha etkili bir şekilde ayarlanmasını sağlar ve optimizasyon sürecini daha kararlı hale getirir.

3. Hızlı ve Stabil Hesaplama

Özellikler ölçeklenmediğinde, SVR’nin hesaplama süresi uzayabilir ve modelin çözümünde kararsızlıklar meydana gelebilir. Özelliklerin ölçeklenmesi hesaplamaların daha hızlı ve stabil olmasını sağlar.

Özetle, SVR ile çalışırken, özelliklerin ölçeklendirilmesi kritik bir adımdır ve genellikle model performansını optimize etmek için gereklidir. Bu nedenle, SVR’yi uygulamadan önce mutlaka veriler ölçeklendirilmelidir.

Sample Application

Bu örnek uygulamada ses verileri ile cinsiyet tanıma işlemini gerçekleştiren bir SVM modeli geliştirilecektir.

Dataset

About the Dataset

Bu veriseti, sesin ve konuşmanın akustik özelliklerine dayanarak bir sesi erkek veya kadın olarak tanımlamak için oluşturulmuştur. Veri seti, erkek ve kadın konuşmacılardan toplanan 3.168 kayıtlı ses örneğinden oluşur. Ses örnekleri, 0hz-280hz (insan ses aralığı) analiz edilmiş bir frekans aralığıyla seewave ve tuneR paketleri kullanılarak R’de akustik analizle önceden işlenir.

Import the necessary modules and libraries

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

from sklearn.preprocessing import StandardScaler, LabelEncoder
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.svm import SVC
from sklearn.metrics import confusion_matrix, classification_report, accuracy_score

import warnings
warnings.filterwarnings("ignore")

Description of Dataset

Read Data

df = pd.read_csv('voice.csv')

print(df.head())

   meanfreq        sd    median       Q25       Q75       IQR       skew  \
0  0.059781  0.064241  0.032027  0.015071  0.090193  0.075122  12.863462   
1  0.066009  0.067310  0.040229  0.019414  0.092666  0.073252  22.423285   
2  0.077316  0.083829  0.036718  0.008701  0.131908  0.123207  30.757155   
3  0.151228  0.072111  0.158011  0.096582  0.207955  0.111374   1.232831   
4  0.135120  0.079146  0.124656  0.078720  0.206045  0.127325   1.101174   

          kurt    sp.ent       sfm  ...  centroid   meanfun    minfun  \
0   274.402906  0.893369  0.491918  ...  0.059781  0.084279  0.015702   
1   634.613855  0.892193  0.513724  ...  0.066009  0.107937  0.015826   
2  1024.927705  0.846389  0.478905  ...  0.077316  0.098706  0.015656   
3     4.177296  0.963322  0.727232  ...  0.151228  0.088965  0.017798   
4     4.333713  0.971955  0.783568  ...  0.135120  0.106398  0.016931   

     maxfun   meandom    mindom    maxdom   dfrange   modindx  label  
0  0.275862  0.007812  0.007812  0.007812  0.000000  0.000000   male  
1  0.250000  0.009014  0.007812  0.054688  0.046875  0.052632   male  
2  0.271186  0.007990  0.007812  0.015625  0.007812  0.046512   male  
3  0.250000  0.201497  0.007812  0.562500  0.554688  0.247119   male  
4  0.266667  0.712812  0.007812  5.484375  5.476562  0.208274   male  

[5 rows x 21 columns]

Describe the data

print(df.describe())

          meanfreq           sd       median          Q25          Q75  \
count  3168.000000  3168.000000  3168.000000  3168.000000  3168.000000   
mean      0.180907     0.057126     0.185621     0.140456     0.224765   
std       0.029918     0.016652     0.036360     0.048680     0.023639   
min       0.039363     0.018363     0.010975     0.000229     0.042946   
25%       0.163662     0.041954     0.169593     0.111087     0.208747   
50%       0.184838     0.059155     0.190032     0.140286     0.225684   
75%       0.199146     0.067020     0.210618     0.175939     0.243660   
max       0.251124     0.115273     0.261224     0.247347     0.273469   

               IQR         skew         kurt       sp.ent          sfm  \
count  3168.000000  3168.000000  3168.000000  3168.000000  3168.000000   
mean      0.084309     3.140168    36.568461     0.895127     0.408216   
std       0.042783     4.240529   134.928661     0.044980     0.177521   
min       0.014558     0.141735     2.068455     0.738651     0.036876   
25%       0.042560     1.649569     5.669547     0.861811     0.258041   
50%       0.094280     2.197101     8.318463     0.901767     0.396335   
75%       0.114175     2.931694    13.648905     0.928713     0.533676   
max       0.252225    34.725453  1309.612887     0.981997     0.842936   

              mode     centroid      meanfun       minfun       maxfun  \
count  3168.000000  3168.000000  3168.000000  3168.000000  3168.000000   
mean      0.165282     0.180907     0.142807     0.036802     0.258842   
std       0.077203     0.029918     0.032304     0.019220     0.030077   
min       0.000000     0.039363     0.055565     0.009775     0.103093   
25%       0.118016     0.163662     0.116998     0.018223     0.253968   
50%       0.186599     0.184838     0.140519     0.046110     0.271186   
75%       0.221104     0.199146     0.169581     0.047904     0.277457   
max       0.280000     0.251124     0.237636     0.204082     0.279114   

           meandom       mindom       maxdom      dfrange      modindx  
count  3168.000000  3168.000000  3168.000000  3168.000000  3168.000000  
mean      0.829211     0.052647     5.047277     4.994630     0.173752  
std       0.525205     0.063299     3.521157     3.520039     0.119454  
min       0.007812     0.004883     0.007812     0.000000     0.000000  
25%       0.419828     0.007812     2.070312     2.044922     0.099766  
50%       0.765795     0.023438     4.992188     4.945312     0.139357  
75%       1.177166     0.070312     7.007812     6.992188     0.209183  
max       2.957682     0.458984    21.867188    21.843750     0.932374  

print(df.columns)

Index(['meanfreq', 'sd', 'median', 'Q25', 'Q75', 'IQR', 'skew', 'kurt',
       'sp.ent', 'sfm', 'mode', 'centroid', 'meanfun', 'minfun', 'maxfun',
       'meandom', 'mindom', 'maxdom', 'dfrange', 'modindx', 'label'],
      dtype='object')

print(df.label.value_counts()) # Count of each label

label
male      1584
female    1584
Name: count, dtype: int64

print(df.info())

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 3168 entries, 0 to 3167
Data columns (total 21 columns):
 #   Column    Non-Null Count  Dtype  
---  ------    --------------  -----  
 0   meanfreq  3168 non-null   float64
 1   sd        3168 non-null   float64
 2   median    3168 non-null   float64
 3   Q25       3168 non-null   float64
 4   Q75       3168 non-null   float64
 5   IQR       3168 non-null   float64
 6   skew      3168 non-null   float64
 7   kurt      3168 non-null   float64
 8   sp.ent    3168 non-null   float64
 9   sfm       3168 non-null   float64
 10  mode      3168 non-null   float64
 11  centroid  3168 non-null   float64
 12  meanfun   3168 non-null   float64
 13  minfun    3168 non-null   float64
 14  maxfun    3168 non-null   float64
 15  meandom   3168 non-null   float64
 16  mindom    3168 non-null   float64
 17  maxdom    3168 non-null   float64
 18  dfrange   3168 non-null   float64
 19  modindx   3168 non-null   float64
 20  label     3168 non-null   object 
dtypes: float64(20), object(1)
memory usage: 519.9+ KB
None

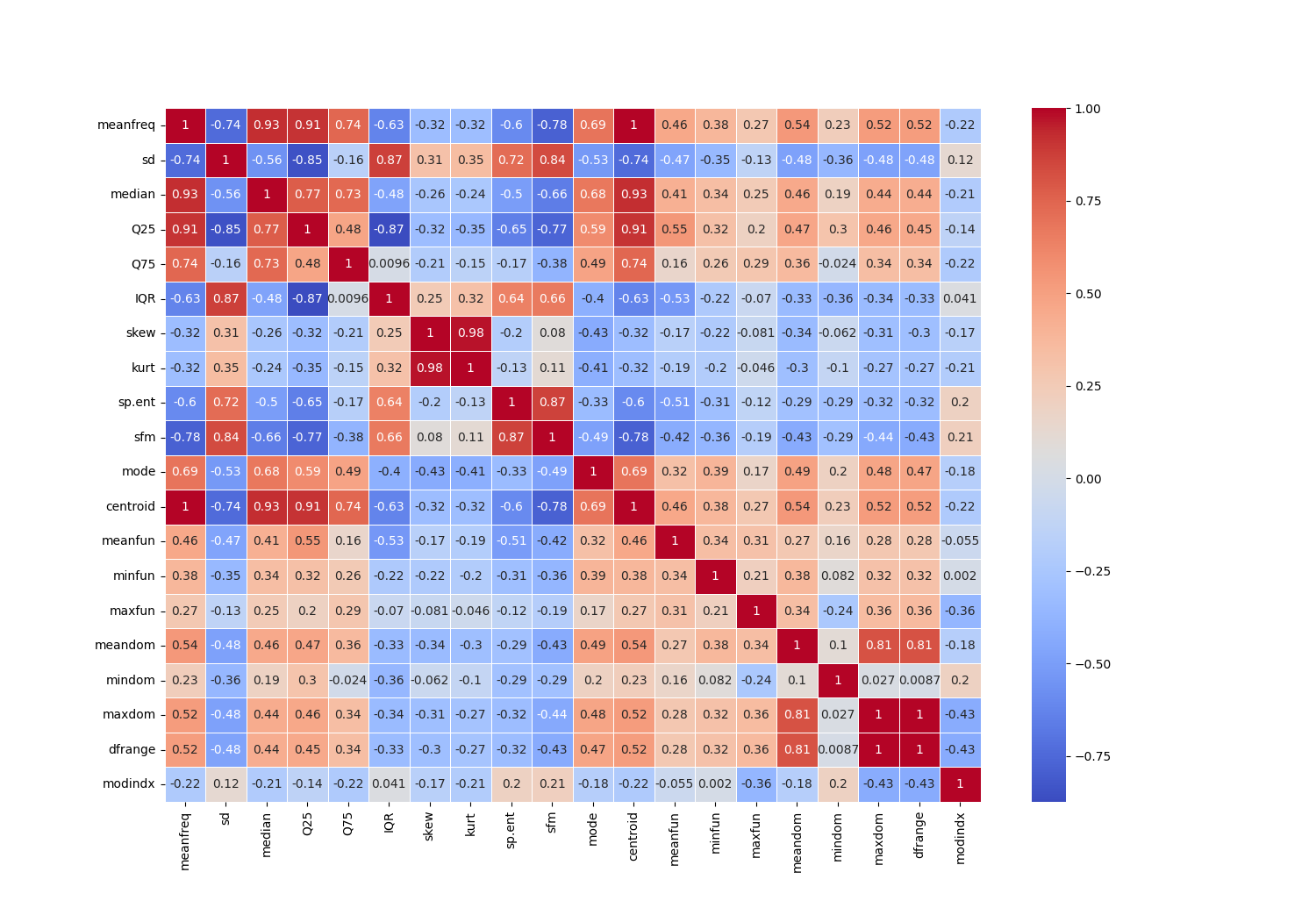
Checking the correlation between each feature

corr = df.drop('label', axis=1).corr()

plt.figure(figsize=(15, 15), dpi=100)
sns.heatmap(corr, annot=True, cmap='coolwarm', linewidths=0.5)

plt.show()

gender recognition by voice dataset corr

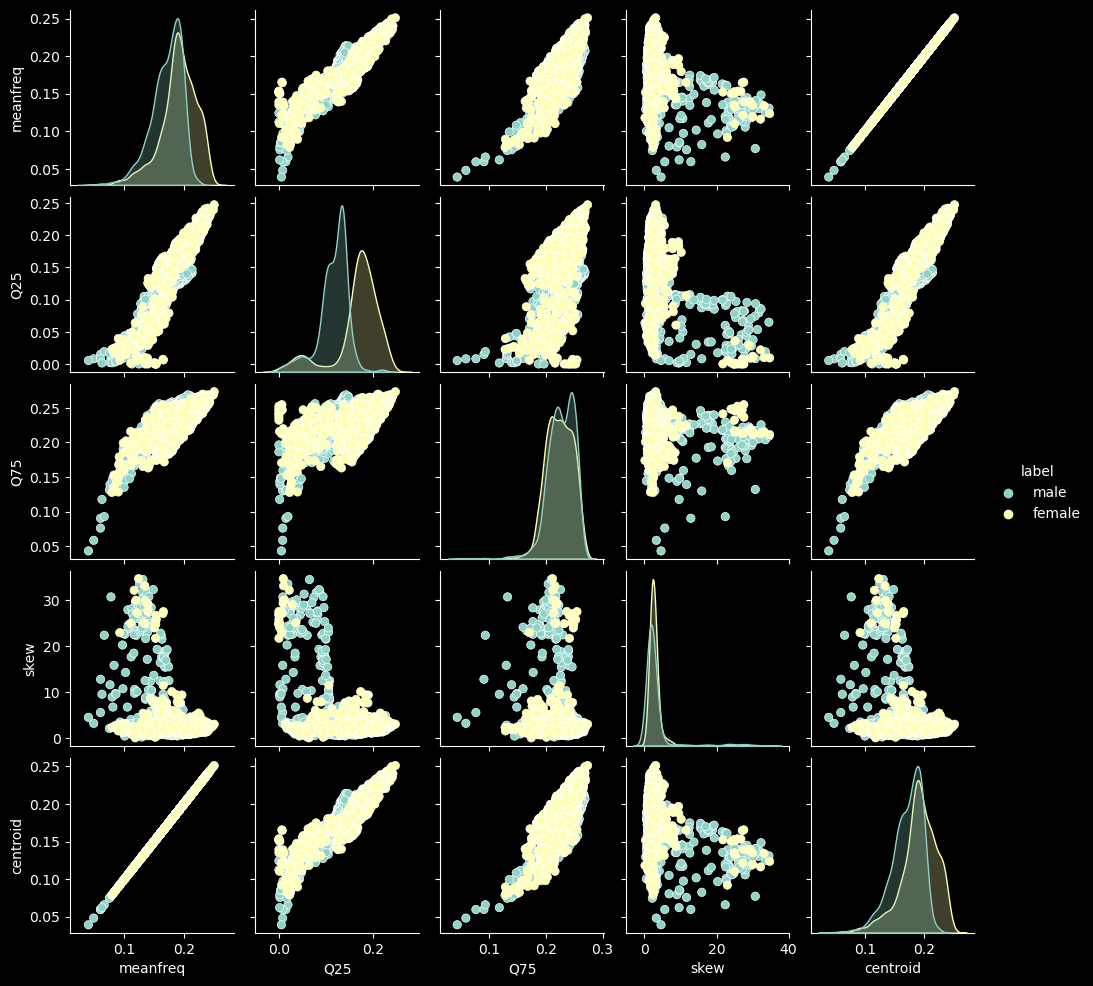
Graphical analysis of data

sns.pairplot(df[['meanfreq', 'Q25', 'Q75', 'skew', 'centroid', 'label']], hue='label', size=2)

gender recognition by voice dataset pairplot graph

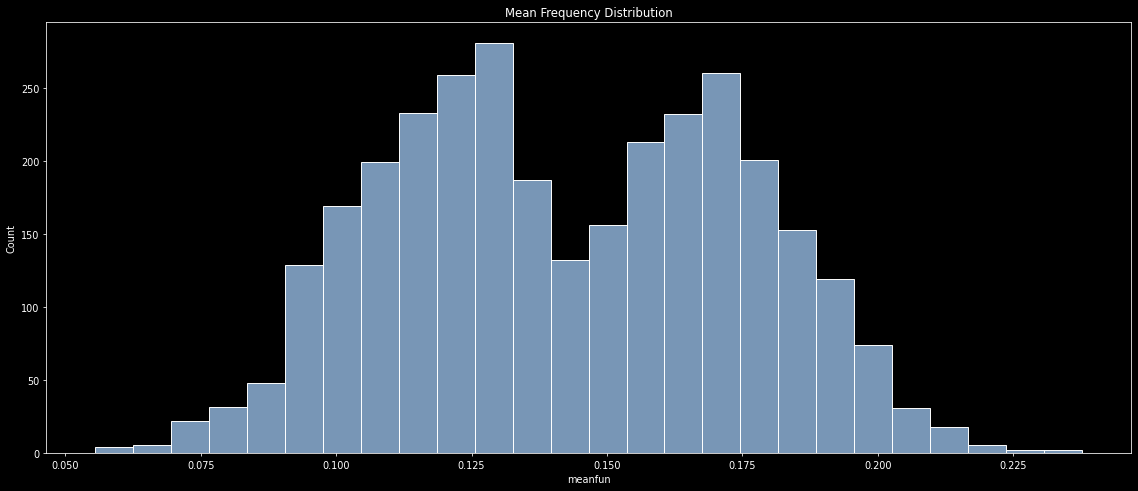
# Distribution of each feature

plt.figure(figsize=(20, 8), dpi=70)
sns.histplot(df.meanfun, color=sns.color_palette('pastel')[0])
plt.title('Mean Frequency Distribution')
plt.show()

gender recognition by voice dataset distribition

Data Preprocessing

Check for missing values

print(df.isnull().sum())

meanfreq    0
sd          0
median      0
Q25         0
Q75         0
IQR         0
skew        0
kurt        0
sp.ent      0
sfm         0
mode        0
centroid    0
meanfun     0
minfun      0
maxfun      0
meandom     0
mindom      0
maxdom      0
dfrange     0
modindx     0
label       0
dtype: int64

Seperating features and labels

x = df.drop('label', axis=1)
y = df.label

print(x.head())

   meanfreq        sd    median       Q25       Q75       IQR       skew  \
0  0.059781  0.064241  0.032027  0.015071  0.090193  0.075122  12.863462   
1  0.066009  0.067310  0.040229  0.019414  0.092666  0.073252  22.423285   
2  0.077316  0.083829  0.036718  0.008701  0.131908  0.123207  30.757155   
3  0.151228  0.072111  0.158011  0.096582  0.207955  0.111374   1.232831   
4  0.135120  0.079146  0.124656  0.078720  0.206045  0.127325   1.101174   

          kurt    sp.ent       sfm      mode  centroid   meanfun    minfun  \
0   274.402906  0.893369  0.491918  0.000000  0.059781  0.084279  0.015702   
1   634.613855  0.892193  0.513724  0.000000  0.066009  0.107937  0.015826   
2  1024.927705  0.846389  0.478905  0.000000  0.077316  0.098706  0.015656   
3     4.177296  0.963322  0.727232  0.083878  0.151228  0.088965  0.017798   
4     4.333713  0.971955  0.783568  0.104261  0.135120  0.106398  0.016931   

     maxfun   meandom    mindom    maxdom   dfrange   modindx  
0  0.275862  0.007812  0.007812  0.007812  0.000000  0.000000  
1  0.250000  0.009014  0.007812  0.054688  0.046875  0.052632  
2  0.271186  0.007990  0.007812  0.015625  0.007812  0.046512  
3  0.250000  0.201497  0.007812  0.562500  0.554688  0.247119  
4  0.266667  0.712812  0.007812  5.484375  5.476562  0.208274

Encoding the labels

# Encode label category
# male -> 1
# female -> 0

le = LabelEncoder()
y = le.fit_transform(y)

print(y)

[1 1 1 ... 0 0 0]

Standardize features

scaler = StandardScaler()
x = scaler.fit_transform(x)

Splitting dataset into training and testing set

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)

Şimdi linear, polynomial ve rbf kernelleri ile birer SVM modeli oluşturup bu modellerin metriklerine bakarak en uygun kerneli seçelim.

Create SVM model with linear kernel and default parameters

linear_svc = SVC(kernel='linear')

linear_svc.fit(x_train, y_train)

SVC(kernel='linear')
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Accuracy of linear model

# Accuracy of model
linear_y_pred = linear_svc.predict(x_test)

print('Accuracy of linear model:', accuracy_score(y_test, linear_y_pred))

Accuracy of linear model: 0.973186119873817

print(classification_report(y_test, linear_y_pred))

              precision    recall  f1-score   support

           0       0.98      0.96      0.97       301
           1       0.96      0.98      0.97       333

    accuracy                           0.97       634
   macro avg       0.97      0.97      0.97       634
weighted avg       0.97      0.97      0.97       634

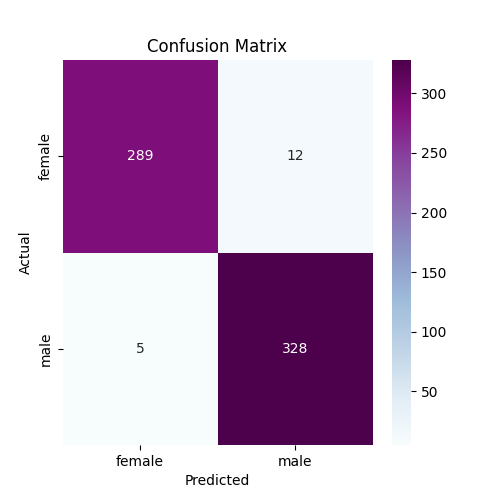
linear_cm = confusion_matrix(y_test, linear_y_pred)

plt.figure(figsize=(5,5))
sns.heatmap(linear_cm, annot=True, cmap='BuPu', fmt='d', xticklabels=['female', 'male'], yticklabels=['female', 'male'])
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.title('Confusion Matrix')
plt.show()

confusion matrix of linear kernel

Create SVM model with polynomial kernel and default parameters

# Create polynomial model with default parameters
poly_svc = SVC(kernel='poly')

poly_svc.fit(x_train, y_train)

SVC(kernel='poly')
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Accuracy of polynomial model

## Accuracy of polynomial model
poly_y_pred = poly_svc.predict(x_test)

print('Accuracy of polynomial model:', accuracy_score(y_test, poly_y_pred))

Accuracy of polynomial model: 0.9589905362776026

print(classification_report(y_test, poly_y_pred))

              precision    recall  f1-score   support

           0       0.98      0.94      0.96       301
           1       0.94      0.98      0.96       333

    accuracy                           0.96       634
   macro avg       0.96      0.96      0.96       634
weighted avg       0.96      0.96      0.96       634

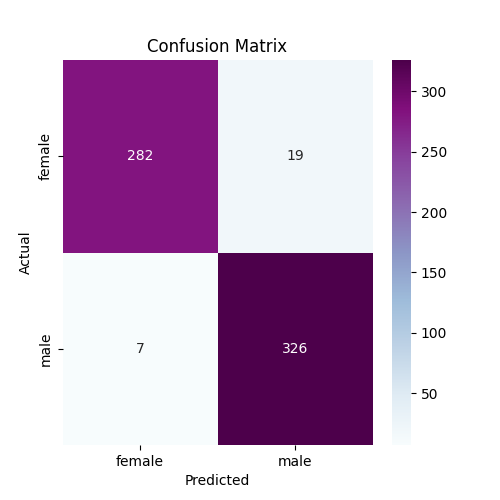
poly_cm = confusion_matrix(y_test, poly_y_pred)

plt.figure(figsize=(5, 5))
sns.heatmap(poly_cm, annot=True, cmap='BuPu', fmt='d', xticklabels=['female', 'male'], yticklabels=['female', 'male'])
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.title('Confusion Matrix')
plt.show()

confusion matrix of polynomial kernel

Create SVM model with rbf kernel and default parameters

rbf_svc = SVC(kernel='rbf')

rbf_svc.fit(x_train, y_train)

SVC()
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Accuracy of rbf model

rbf_y_pred = rbf_svc.predict(x_test)

print('Accuracy of rbf model:', accuracy_score(y_test, rbf_y_pred))

Accuracy of rbf model: 0.9842271293375394

print(classification_report(y_test, rbf_y_pred))

              precision    recall  f1-score   support

           0       0.98      0.99      0.98       301
           1       0.99      0.98      0.98       333

    accuracy                           0.98       634
   macro avg       0.98      0.98      0.98       634
weighted avg       0.98      0.98      0.98       634

# Confusion matrix with seaborn heatmap
rbf_cm = confusion_matrix(y_test, rbf_y_pred)

plt.figure(figsize=(5,5))
sns.heatmap(rbf_cm, annot=True, cmap='BuPu', fmt='d', xticklabels=['female', 'male'], yticklabels=['female', 'male'])
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.title('Confusion Matrix')
plt.show()

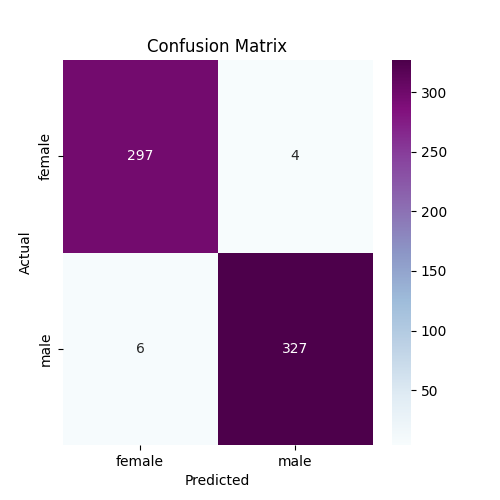
confision matrix of rbf kernel

Metriklerden ve matrislerden de anlaşılacağı üzere RBF kernel fonksiyonu ile oluşturulan SVM modeli daha kabul edilebilir tahminler yaptı.

Ancak bu modeller default hiperparametreler ile oluşturulduğu için en iyi sonucu RBF kernel ile oluşturulmuş modelin verdiğini her zaman söyleyemeyiz. Çünkü diğer kerneller ile de oluşturulmuş olan modellerin parametreleri (C, gamma, degree) ile oynayarak daha iyi bir sonuç elde etme ihtimali var.

C, gamma ve degree parametreleri, modelin davranışını kontrol eden önemli hiperparametrelerdir. Bu parametreler, modelin doğruluğunu ve genelleme yeteneğini etkiler. Hangi kernel fonksiyonunun seçildiğine bağlı olarak bu parametreler farklı şekillerde kullanılır.

C parametresi

C parametresi, modelin hata toleransı ve marjin genişliği arasında bir denge kurar. C değeri, modelin ne kadar hata yapmasına izin verileceğini ve marjinin ne kadar geniş olacağını kontrol eder.

Küçük C Değeri

Daha geniş bir marjin tercih edilir ve bazı veri noktalarının yanlış sınıflandırılmasına izin verilir. Bu, modelin genelleme yeteneğini artırabilir, ancak hatalı sınıflandırmalar meydana gelebilir.

Büyük C Değeri

Hatalara karşı tolerans azalır, yani model daha katı bir şekilde veriyi doğru sınıflandırmaya çalışır. Bu, daha dar bir marjine yol açabilir, ancak aşırı öğrenme (overfitting) riski taşır.

Özet

  • Küçük C: Geniş marjin, daha fazla genelleme, potansiyel yanlış sınıflandırmalar.
  • Büyük C: Dar marjin, az genelleme, daha fazla doğru sınıflandırma, aşırı öğrenme riski.

gamma parametresi

Gamma parametresi, özellikle RBF (Radial Basis Function), Polynomial ve Sigmoid gibi doğrusal olmayan kernel fonksiyonlarında kullanılır. Gamma, modelin her bir eğitim örneğinin ne kadar etkili olacağını kontrol eder. Gamma değeri, modelin karar sınırlarını belirler ve yüksek veya düşük değerler modelin performansını büyük ölçüde etkileyebilir.

  • Küçük gamma değeri: Küçük gamma değeri, her bir veri noktasının uzak mesafedeki diğer veri noktalarını da etkileyebilmesi anlamına gelir. Bu, daha düzgün ve geniş bir karar sınırı sağlar. Ancak, düşük bir gamma değeri, modelin karmaşık verileri doğru şekilde ayırmada başarısız olmasına yol açabilir.

  • Büyük gamma değeri: Büyük gamma değeri, her veri noktasının sadece yakın çevresindeki noktaları etkilemesine neden olur. Bu, karar sınırlarının daha keskin olmasını sağlar ve model veriyi daha sıkı bir şekilde öğrenir. Ancak, bu durum aşırı öğrenmeye (overfitting) yol açabilir.

Özet

  • Küçük gamma: Karar sınırları daha geniş ve basit, daha iyi genelleme, düşük hassasiyet.
  • Büyük gamma: Karar sınırları daha keskin, yüksek hassasiyet, aşırı öğrenme riski.

degree parametresi

degree parametresi, yalnızca Polynomial kernel ile birlikte kullanılır ve polinomun derecesini belirtir. Yani, veriyi ayırmak için kullanılan polinomun derecesini belirler. Doğrusal olmayan sınırları modellemek için polinomsal bir yaklaşım kullanıyorsanız, polinomun derecesi bu parametre ile kontrol edilir.

Küçük degree değeri

Küçük bir degree değeri, veriyi ayırmak için daha basit (örneğin, doğrusal) sınırlar oluşturur. Bu, daha hızlı bir model sağlar ancak karmaşık veri yapıları için yeterli olmayabilir.

Büyük degree değeri

Yüksek degree değeri, daha karmaşık polinomsal sınırlar oluşturur. Bu, daha karmaşık veri kümelerini daha doğru sınıflandırabilir, ancak modelin aşırı uyum gösterme riski artar.

Özet

  • Küçük degree: Daha basit karar sınırları, düşük doğruluk (karmaşık veriler için), daha hızlı hesaplama.
  • Büyük degree: Daha karmaşık karar sınırları, aşırı öğrenme riski, daha yavaş hesaplama.

Sonuç: Hangi Durumda Hangi Parametre

  • C Parametresi: Hata toleransı ile marjin genişliği arasında bir denge sağlar. Genelleme yeteneğini kontrol etmek için kullanılır.
  • gamma Parametresi: Özellikle RBF kernelde her veri noktasının etki alanını belirler. Karar sınırlarının ne kadar keskin olacağını kontrol eder.
  • degree Parametresi: Sadece Polynomial kernelde kullanılır ve polinomun derecesini belirler, daha karmaşık veri ayrımları yapabilmeyi sağlar.

Bu parametrelerin uygun seçimi, modelin veriyi doğru bir şekilde öğrenip genelleyebilmesi açısından kritik öneme sahiptir. Parametre optimizasyonu için Grid Search veya Randomized Search gibi yöntemlerle bu hiperparametreleri ayarlamak, modelin performansını önemli ölçüde artırabilir.