Logistic Regression
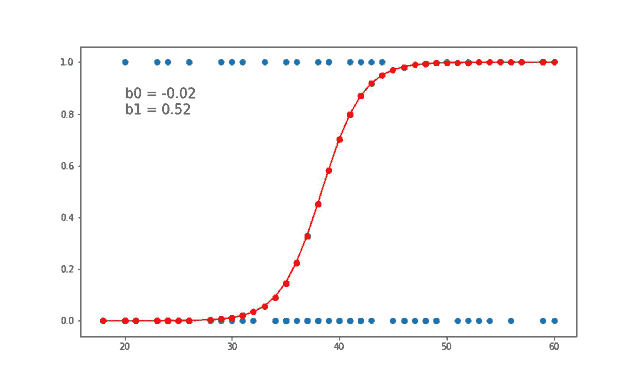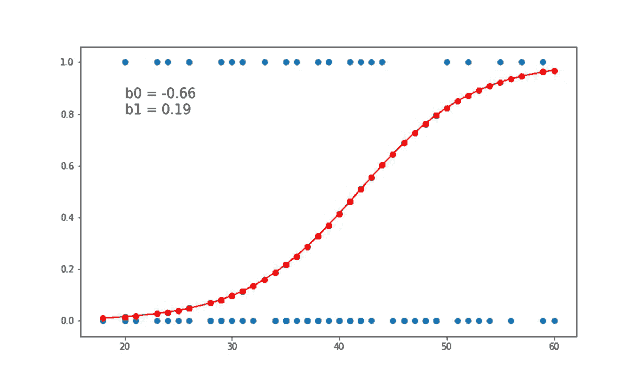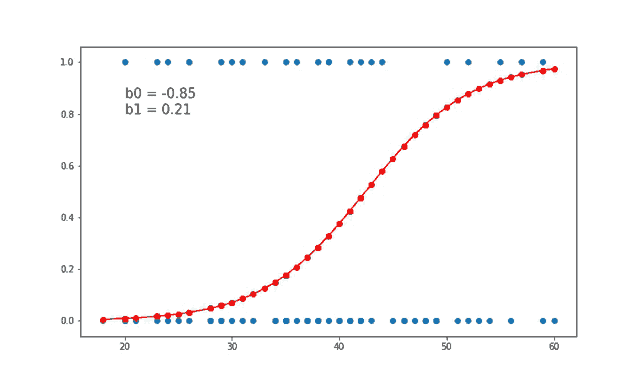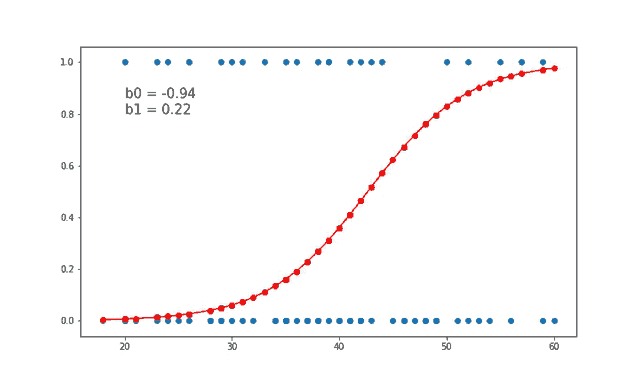
Logistic regression, basit yapısı ve açıklanabilirliği nedeniyle makine öğrenmesi uygulamalarında sıkça tercih edilen bir algoritmadır. Temel sınıflandırma problemlerinde etkili bir çözümdür ve daha karmaşık modellerin anlaşılmasında temel bir yapı taşı olarak görev yapar.
- 1. Temel Kavramlar
- 2. Matematiksel Temel
- 3. Çoklu Sınıf Problemleri (Multinomial Logistic Regression)
- 4. Örnek Uygulama
- Dataset
- Import the necessary modules and libraries
- Data Preprocessing
- Building and training of the model
- Predict
- Evaluation
- 5. Avantajlar ve Dezavantajlar
Logistic regression, makine öğrenmesinde kullanılan en temel sınıflandırma algoritmalarından biridir. Lineer regresyon ile benzer temellere dayansa da, logistic regression sınıflandırma problemleri için uygundur. Özellikle iki sınıf (binary) arasındaki ayrımı yapmak için kullanılır, ancak birden fazla sınıf için de genişletilebilir (multinomial logistic regression).
1. Temel Kavramlar
Logistic regression, doğrusal bir modeldir, ancak çıkış değeri sürekli bir sayı yerine bir olasılık olarak ifade edilir. Bu, modelin çıkışını 0 ile 1 arasında bir değere dönüştürmek için bir sigmoid fonksiyonu kullanması sayesinde olur.
2. Matematiksel Temel
a. Lineer Model
Logistic regression, bir doğrusal model ile başlar: \[z = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n = \beta_0 + \sum_{i=1}^{n}{\beta_i x_i}\]
Burada \(z\), bağımsız değişkenlerin bir lineer kombinasyonu olarak hesaplanır. Bu, aslında lineer regresyonun hesaplamasından farklı değildir.
b. Sigmoid Fonksiyonu
Logistic regression’ın temel farkı, yukarıdaki doğrusal modelin sonucunu sigmoid fonksiyonu denilen bir fonksiyondan geçirerek olasılıkları hesaplamasıdır: \[h(z) = \frac{1}{1 + {e}^{-z}} = \frac{1}{1 + {e}^{-(\beta_0 + \beta_1 x_1 + \beta_2 x_2 + ... + \beta_n x_n)}}\]
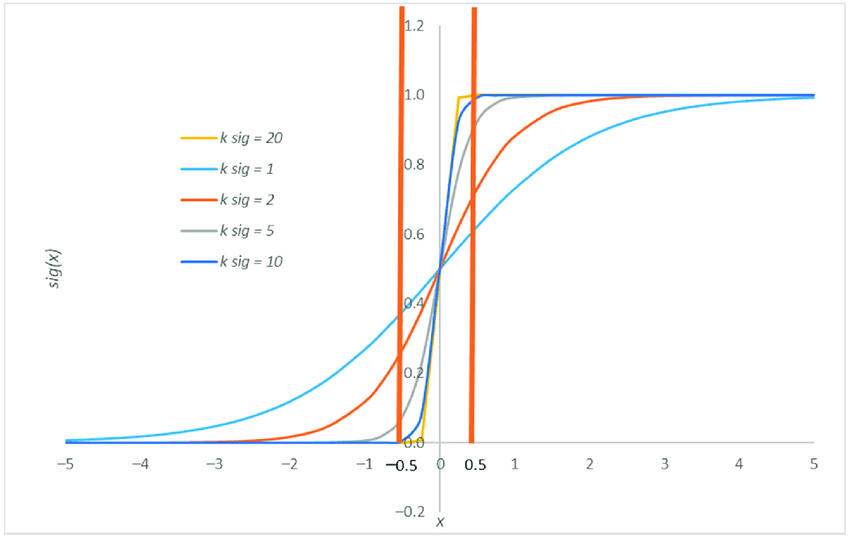
Sigmoid fonksiyonu, her zaman 0 ile 1 arasında bir değer döndürür ve bu da, sınıf 1’e ait olma olasılığı olarak yorumlanır. Eğer olasılık 0.5’ten büyükse, model sınıfı 1 olarak tahmin eder; aksi takdirde 0 olarak tahmin eder.
3. Çoklu Sınıf Problemleri (Multinomial Logistic Regression)
Eğer problemde iki yerine birden fazla sınıf varsa, logistic regression birden fazla sınıfı ayırmak için genişletilebilir. Bu, “one-vs-all” (birine karşı diğerleri) veya “softmax regression” gibi yöntemlerle yapılabilir.
4. Örnek Uygulama
Örneğin, bir kişinin cinsiyetini tahmin etmek için logistic regression kullanılabilir. Girdi olarak kişinin boy, kilo, yaş bilgileri gibi özellikler kullanılır ve model, bu özelliklere dayalı olarak kişinin erkek olup olmadığını (sınıf 1) veya kadın olduğunu (sınıf 0) tahmin eder.
Dataset
// file: "data.csv"
ulke,boy,kilo,yas,cinsiyet
tr,180,90,30,e
tr,190,80,25,e
tr,175,90,35,e
tr,177,60,22,k
us,185,105,33,e
us,165,55,27,k
us,155,50,44,k
us,160,58,39,k
us,162,59,41,k
us,167,62,55,k
fr,174,70,47,e
fr,193,90,23,e
fr,187,80,27,e
fr,183,88,28,e
fr,159,40,29,k
fr,164,66,32,k
fr,166,56,42,k
Import the necessary modules and libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sbn
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix
Data Preprocessing
Read Data
data = pd.read_csv('data.csv')
print(data.head(10))
print(data.describe())
ulke boy kilo yas cinsiyet 0 tr 180 90 30 e 1 tr 190 80 25 e 2 tr 175 90 35 e 3 tr 177 60 22 k 4 us 185 105 33 e 5 us 165 55 27 k 6 us 155 50 44 k 7 us 160 58 39 k 8 us 162 59 41 k 9 us 167 62 55 k boy kilo yas count 17.000000 17.000000 17.000000 mean 173.058824 70.529412 34.058824 std 11.829363 17.871477 9.270050 min 155.000000 40.000000 22.000000 25% 164.000000 58.000000 27.000000 50% 174.000000 66.000000 32.000000 75% 183.000000 88.000000 41.000000 max 193.000000 105.000000 55.000000
Split Data
# boy
boy = data.iloc[:, 1:2].values
# kilo
kilo = data.iloc[:, 2:3].values
# yas
yas = data.iloc[:, 3:4].values
# cinsiyet
cinsiyet = data.iloc[:, -1:].values
Concatenate Data
Şimdi bu boy, kilo ve yas bağımsız değişkenlerini (x) ve cinsiyet (y) bağımlı değişkenini birleştiriyorum.
# Concatenate Data
x = pd.DataFrame(np.concatenate((boy, kilo, yas), axis= 1), columns=['boy', 'kilo', 'yas'])
y = pd.DataFrame(cinsiyet, columns=['cinsiyet'])
print(x.head(5))
print(y.head(5))
boy kilo yas 0 180 90 30 1 190 80 25 2 175 90 35 3 177 60 22 4 185 105 33 cinsiyet 0 e 1 e 2 e 3 k 4 e
Encoding
Eğitim sürecinde kullanılacak cinsiyet (y) bağımlı değişkenini LabelEncoder sınıfı ile sayısal değerlere dönüştürüyorum.
le = LabelEncoder()
y = le.fit_transform(y)
print(y)
[0 0 0 1 0 1 1 1 1 1 0 0 0 0 1 1 1]
Train - Test Split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.33, random_state=0)
Scale Data
sc = StandardScaler()
X_train = sc.fit_transform(x_train)
X_test = sc.transform(x_test)
print(X_train.shape)
print(y_train.shape)
(11, 3) (6, 3)
Building and training of the model
log_reg = LogisticRegression(random_state=0)
log_reg.fit(X_train, y_train)
LogisticRegression(random_state=0)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LogisticRegression(random_state=0)
Predict
y_pred = log_reg.predict(X_test)
for i in range(len(y_pred)):
print(f"Actual Class: {y_test[i]} - Predicted Class: {y_pred[i]}")
Actual Class: 0 - Predicted Class: 0 Actual Class: 1 - Predicted Class: 1 Actual Class: 1 - Predicted Class: 1 Actual Class: 1 - Predicted Class: 1 Actual Class: 0 - Predicted Class: 0 Actual Class: 0 - Predicted Class: 0
Evaluation
# Confusion Matrix
cm = confusion_matrix(y_true=y_test, y_pred=y_pred)
print(cm)
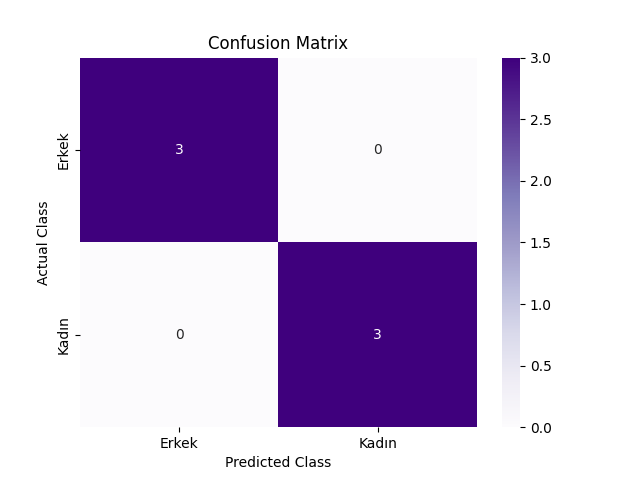
sbn.heatmap(cm, annot=True, fmt='d', cmap='Purples', xticklabels=['Erkek', 'Kadın'], yticklabels=['Erkek', 'Kadın'])
plt.xlabel('Predicted Class')
plt.ylabel('Actual Class')
plt.title('Confusion Matrix')
plt.show()
[[3 0]
[0 3]]
# Accuracy
accuracy = (cm[0][0] + cm[1][1]) / len(y_test)
print(f'Accuracy: {accuracy}')
Accuracy: 1.0
5. Avantajlar ve Dezavantajlar
Avantajlar:
- Basit ve uygulanması kolaydır.
- Sınıflandırma problemleri için oldukça etkilidir.
- Modelin çıktısı bir olasılık verdiği için, karar verici sistemlerde kolayca entegre edilebilir.
Dezavantajlar:
- Non-lineer problemlerde sınırlıdır.
- Veriler arasındaki ilişki doğrusal değilse, performansı düşer.
- Dengesiz veri setlerinde (bir sınıfın diğerinden çok daha fazla olduğu durumlar) performansı düşebilir.