Decision Trees

Categorized under Machine Learning tagged Prediction Last modified at:
Decision Trees

Karar ağaçları (Decision Trees), makine öğrenmesinde yaygın olarak kullanılan bir denetimli öğrenme algoritmasıdır. Hem sınıflandırma hem de regresyon problemlerinde kullanılabilirler.

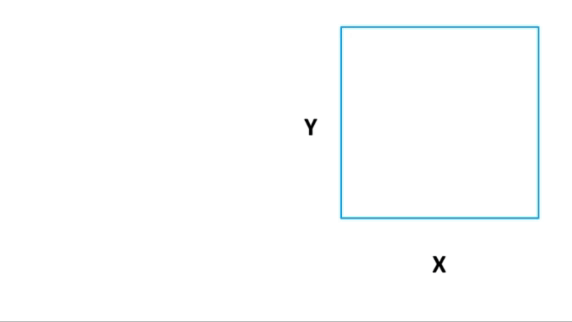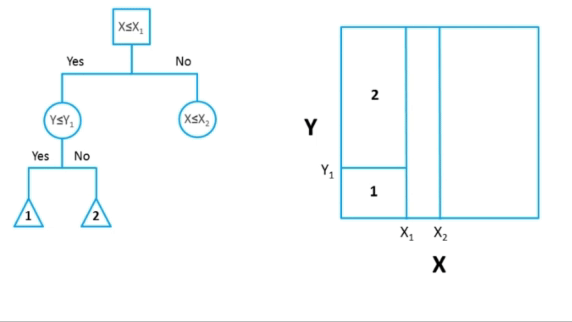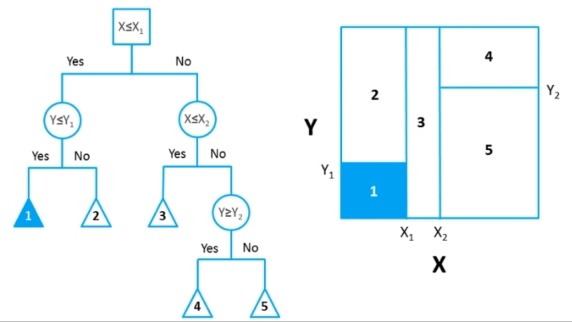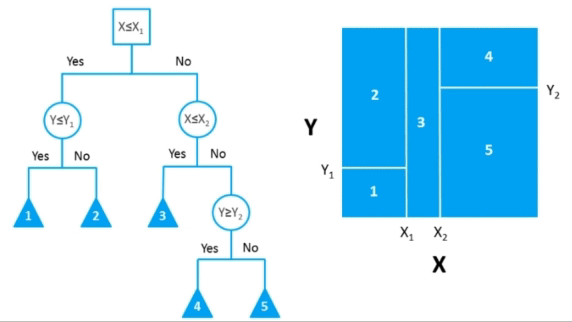
Karar ağaçları, veriyi dallara ayırarak kararlar verir. Ağaç yapısı, kök düğümden (root) başlayarak, her düğümde bir özelliğin (feature) değeri üzerinden bir karar alır ve bu karara göre dallanarak ilerler. Son düğümler (yaprak düğümler) ise sınıflandırma veya regresyon sonuçlarını temsil eder.

1. Temel Kavramlar

  • Kök Düğüm (Root Node): Karar ağacının en üstünde bulunan ve en önemli özellikten ayrılma işlemini başlatan düğümdür. Bu düğüm, tüm veri kümesini temsil eder ve veriyi dallara ayıran ilk soruyu içerir.
  • Dallanma (Branching): Düğümler arasındaki bağlantılardır ve bir özelliğe (örneğin, X > 5) dayalı olarak bir veriyi belirli bir yola yönlendirir. Her düğümde belirli bir özellik üzerinden veri iki veya daha fazla alt gruba ayrılır. Bu süreç, ağacın alt dallarını oluşturur.
  • Yaprak Düğüm (Leaf Node): Karar ağacının sonuna ulaşmış olan düğümlerdir. Bu düğümler, nihai sınıflandırmayı veya tahmini temsil eder. Bu düğümler, sınıflandırma probleminde bir sınıf etiketini, regresyon probleminde ise bir sayısal değeri temsil eder.
  • Derinlik (Depth): Ağacın kök düğümden en derindeki yaprak düğüme kadar olan yolun uzunluğu, ağacın derinliğini ifade eder.

2. Çalışma Prensibi

1. Veri Kümelerinin Bölümlenmesi

  • Karar ağacı, veri kümesini, her bir özellik için en iyi bölmeyi arar. Bu bölme, her bir özelliğin belirli bir eşik değerine göre (örneğin, X > 5) veriyi ikiye ayırmasıyla oluşur.

2. Bölme Kriterleri

  • Karar ağacının en iyi bölmeyi bulmak için kullandığı ölçütler vardır. Bu ölçütler, veri kümesini en saf hale getiren bölmeyi seçmek amacıyla kullanılır.

Sınıflandırma için kullanılan ölçütler:

Gini Katsayısı :

Bir veri kümesinin saflığını ölçer. Düşük Gini, daha saf bir küme demektir. Bir veri kümesindeki sınıf dağılımı ne kadar homojense, Gini katsayısı o kadar düşük olur. \[Gini(D) = 1 - \sum_{i=1}^{C}{p_i^2}\]

  • \(D\) : Veri kümesi
  • \(C\) : Sınıf sayısı
  • \(p_i\) : \(i\)-inci sınıfa ait olma olasılığı

Örnek: Eğer bir veri kümesinde iki sınıf varsa ve her iki sınıfın da olasılığı 0.5 ise: \[Gini(D) = 1 - (0.5^2 + 0.5^2) = 1 - (0.25 + 0.25) = 1 - 0.5 = 0.5\]

Bilgi Kazancı (Information Gain):

Bilgi kazancı, entropi kavramına dayanır ve bir bölme işleminden önce ve sonra veri kümesindeki düzensizliğin (entropi) ne kadar azaldığını ölçer.

  • Entropi: Entropi, bir veri kümesinin düzensizliğini ölçer. Entropi ne kadar yüksekse, veri kümesi o kadar karışıktır.
\[Entropy(D) = - \sum_{i=1}^{C}{p_i * log_2(p_i)}\]
  • \(D\) : Veri kümesi
  • \(C\) : Sınıf sayısı

  • \(p_i\) : \(i\)-inci sınıfa ait olma olasılığı

  • Bilgi Kazancı (Information Gain): Bir özelliğin (feature) bölme işleminden sonra veri kümesindeki entropiyi ne kadar azalttığını ölçer.
\[Information Gain(D,A) = Entropy(D) - \sum_{v \in values(A)}{\frac{|D_v|}{|D|} * Entropy(D_v)}\]
  • \(A\) : Bölme yapılan özellik
  • \(values(A)\) : Özellik \(A\)‘nın alabileceği tüm değerler
  • \(\lvert D \rvert\) : Veri kümesinin boyutu
  • \(\lvert D_v \rvert\) : \(v\) değerine sahip alt veri kümesinin boyutu

Örnek : Eğer bir veri kümesi için başlangıç entropisi 0.94 ve bölme işleminden sonra iki alt veri kümesi oluşuyorsa (her biri entropisi 0.5 olan), bilgi kazancı şu şekilde hesaplanır: \[Information Gain(D,A) = 0.94 - (\frac{1}{2} * 0.5 + \frac{1}{2} * 0.5) = 0.94 - 0.5 = 0.44\]

Regresyon için kullanılan ölçütler :

1. Ortalama Kare Hatası (Mean Squared Error, MSE):

Ortalama kare hatası, regresyon problemlerinde kullanılır ve tahmin edilen değerlerin gerçek değerlerden ortalama olarak ne kadar saptığını ölçer. Hedef, bu değeri en aza indirmektir. \[MSE = \frac{1}{n}\sum_{i=1}^{n}{(y_i - \hat{y_i})}^2\]

  • \(n\) : Veri kümesindeki örnek sayısı
  • \(y_i\) : Gerçek değer
  • \(\hat{y_i}\) : Tahmin edilen değer

2. Ortalama Mutlak Hata (Mean Absolute Error, MAE)

Ortalama mutlak hata da regresyon problemlerinde kullanılır ve tahmin edilen değerlerin gerçek değerlerden ortalama olarak ne kadar saptığını ölçer, ancak bu sefer mutlak değerler üzerinden hesaplama yapılır. \[MAE = \frac{1}{n}\sum_{i=1}^{n}{|y_i - \hat{y_i}|}\]

  • \(n\) : Veri kümesindeki örnek sayısı
  • \(y_i\) : Gerçek değer
  • \(\hat{y_i}\) : Tahmin edilen değer

Bu denklemler, karar ağacı modellerinde hangi bölmenin daha iyi olduğuna karar vermek için kullanılır ve modelin doğruluğunu artırmaya yardımcı olur.

3. Ağacın Büyümesi

Karar ağacı, veri kümesini dallara ayırmaya devam eder ve her dalın sonunda karar düğümlerini oluşturur. Ağaç, belirli bir durdurma kriterine (örneğin, maksimum derinlik, minimum yaprak düğüm sayısı) ulaşana kadar büyür.

4. Tahmin

Yeni bir veri geldiğinde, karar ağacı bu veriyi kök düğümden başlatarak dallar boyunca yönlendirir ve en sonunda yaprak düğümünde bir tahmin üretir.

3. Karar Ağaçlarının İyileştirilmesi

1. Budama (Pruning):

Aşırı uyumu önlemek için ağacın bazı dallarını kesme işlemidir. Bu, genellikle daha küçük ve daha genellenebilir bir ağaç oluşturur.

2. Çanta Yöntemi (Bagging) ve Rastgele Ormanlar (Random Forests):

Birden fazla karar ağacı oluşturup, bu ağaçların tahminlerini birleştirerek daha dengeli ve güçlü bir model elde edilir.

3. Öznitelik Seçimi:

Karar ağacının aşırı uyumunu önlemek için, modelin yalnızca en etkili özellikleri kullanmasına izin verilir.

Bu şekilde, karar ağaçları makine öğreniminde güçlü bir araç olarak yerini alır, ancak dikkatli bir şekilde ayarlandığında ve diğer yöntemlerle birleştirildiğinde en iyi sonuçları verir.

Şimdi salaries.csv verisetimizdeki eğitim seviyesi bağımsız değişkeni (X) ile maaş bağımlı değişkenini (Y) tahmin eden bir karar ağacı modeli oluşturalım.

Dataset

salaries.csv

Import the necessary modules and libraries

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sbn
from sklearn.tree import DecisionTreeRegressor

Data Preprocessing

Read Data

data = pd.read_csv('salaries.csv')

print(data)

              unvan  Egitim Seviyesi   maas
0             Cayci                1   2250
1          Sekreter                2   2500
2  Uzman Yardimcisi                3   3000
3             Uzman                4   4000
4  Proje Yoneticisi                5   5500
5               Sef                6   7500
6             Mudur                7  10000
7          Direktor                8  15000
8           C-level                9  25000
9               CEO               10  50000

Graphical Analysis of Data

sbn.pairplot(data)

seaborn graph

Split Data

egitim_seviyesi_X = data.iloc[:,1:2].values
maas_Y = data.iloc[:,2:].values

for i in range(len(egitim_seviyesi_X)):
    print("Egitim Seviyesi: ",egitim_seviyesi_X[i],"Maas: ",maas_Y[i])

Egitim Seviyesi:  [1] Maas:  [2250]
Egitim Seviyesi:  [2] Maas:  [2500]
Egitim Seviyesi:  [3] Maas:  [3000]
Egitim Seviyesi:  [4] Maas:  [4000]
Egitim Seviyesi:  [5] Maas:  [5500]
Egitim Seviyesi:  [6] Maas:  [7500]
Egitim Seviyesi:  [7] Maas:  [10000]
Egitim Seviyesi:  [8] Maas:  [15000]
Egitim Seviyesi:  [9] Maas:  [25000]
Egitim Seviyesi:  [10] Maas:  [50000]

Creating the Model

Şimdi DecisionTreeRegressor sınıfını kullanarak bir karar ağacı oluşturalım. Bu sınıfı kullanırken aldığı parametreler modelin nasıl inşa edileceğini belirler.

dtr_1 = DecisionTreeRegressor(criterion='squared_error',
                            splitter='best',
                            max_depth=None,
                            min_samples_split=2,
                            min_samples_leaf=1,
                            min_weight_fraction_leaf=0.0,
                            max_features=None,
                            random_state=None,
                            max_leaf_nodes=None,
                            min_impurity_decrease=0.0,
                            ccp_alpha=0.0)

Parameters

1. criterion='squared_error' :

  • Açıklama : Bölme kalitesini değerlendirmek için kullanılan fonksiyondur. Varsayılan olarak 'squared_error' kullanılır, bu da ortalama kare hatayı minimize etmeye çalışır.
  • Diğer seçenekler : Diğer seçenekler: friedman_mse, absolute_error, poisson.

2. splitter='best' :

  • Açıklama : Düğümleri nasıl böleneceğini belirler. best seçeneği, her düğüm için en iyi bölmeyi seçer. random seçeneği ise bölmeyi rastgele seçer.

3. max_depth=None :

  • Açıklama : Ağacın maksimum derinliğini belirler. Derinlik arttıkça model karmaşıklığı da artar, ancak aşırı öğrenme (overfitting) riski de artar. None değeri, ağacın yaprak düğümleri saf olana kadar büyümesine izin verir.

4. min_samples_split=2 :

  • Açıklama : Bir düğümün bölünmesi için gereken minimum örnek sayısını belirler. Daha büyük bir sayı, daha az bölünmeye ve daha basit bir model elde edilmesine neden olabilir.

5. min_samples_leaf=1 :

  • Açıklama : Yaprak düğümde bulunması gereken minimum örnek sayısını belirler. Bu parametreyi artırmak, daha az sayıda yaprak düğüm oluşturur.

6. min_weight_fraction_leaf=0.0 :

  • Açıklama : Yaprak düğümde bulunması gereken minimum ağırlık oranını belirler. Örneğin, sınıflandırmada sınıflar arası dengesizliği kontrol etmek için kullanılabilir.
  • Kullanımı : Float (0.0 ile 0.5 arasında).

7. max_features=None :

  • Açıklama : Her bölme için göz önünde bulundurulacak maksimum özellik sayısını belirler. None değeri, tüm özelliklerin kullanılacağı anlamına gelir.
  • Diğer seçenekler : 'auto', 'sqrt', 'log2' veya pozitif bir tam sayı.

8. random_state=None :

  • Açıklama : Rastgelelik unsurlarını kontrol etmek için kullanılır. Aynı random_state değeri ile tekrarlandığında aynı sonuçlar elde edilir.
  • Kullanımı : Bir tamsayı veya None.

9. max_leaf_nodes=None :

  • Açıklama : Yaprak düğümlerin maksimum sayısını belirler. Bu parametre ağaç boyutunu kontrol eder ve aşırı öğrenmeyi önlemeye yardımcı olabilir.
  • Kullanımı : Pozitif bir tamsayı veya None.

10. min_impurity_decrease=0.0 :

  • Açıklama : Bölme yapılabilmesi için gereken minimum kirlilik azalmasını belirtir. Bu değerin artırılması, daha az sayıda bölme yapılmasına yol açar.

11. ccp_alpha=0.0 :

  • Açıklama : Karışıklık karmaşıklığını budama için kullanılan bir parametredir. Budama işlemi sırasında kullanılan alpha değeri büyüdükçe, daha fazla düğüm budanır.

Bu parametreler, DecisionTreeRegressor modelinin esnekliğini ve performansını ayarlamak için kullanılır. Hangi parametrelerin hangi değerlerde seçileceği, genellikle veri setinin özelliklerine ve modelleme amacına bağlıdır.

Fit regression model

dtr_1.fit(egitim_seviyesi_X, maas_Y)

DecisionTreeRegressor()
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Predict

predict_1 = dtr_1.predict(egitim_seviyesi_X)

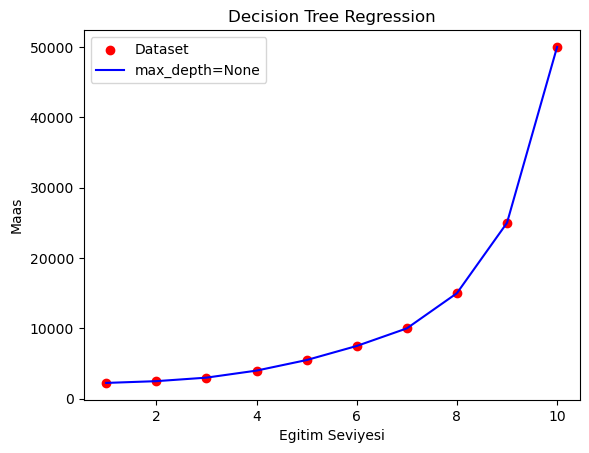
Plot the results

plt.scatter(egitim_seviyesi_X, maas_Y, color='red', label='Dataset')
plt.plot(egitim_seviyesi_X, predict_1, color='blue', label='max_depth=None')
plt.title('Decision Tree Regression')
plt.xlabel('Egitim Seviyesi')
plt.ylabel('Maas')
plt.legend()
plt.show()

decision tree regression plot

Şimdi max_depth=None parametresinin değerini max_depth=2 olarak değiştirerek derinliği 2 olan yeni bir karar ağacı modeli oluşturalım ve test edelim.

Creating the new model

dtr_2 = DecisionTreeRegressor(criterion='squared_error',
                            splitter='best',
                            max_depth=2,
                            min_samples_split=2,
                            min_samples_leaf=1,
                            min_weight_fraction_leaf=0.0,
                            max_features=None,
                            random_state=None,
                            max_leaf_nodes=None,
                            min_impurity_decrease=0.0,
                            ccp_alpha=0.0)

Fit regression model

dtr_2.fit(egitim_seviyesi_X, maas_Y)

DecisionTreeRegressor(max_depth=2)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Predict

predict_2 = dtr_2.predict(egitim_seviyesi_X)

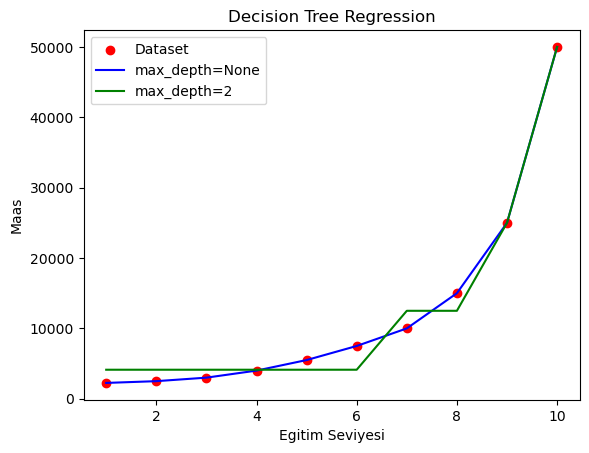
Plot the results

plt.scatter(egitim_seviyesi_X, maas_Y, color='red', label='Dataset')
plt.plot(egitim_seviyesi_X, predict_1, color='blue', label='max_depth=None')
plt.plot(egitim_seviyesi_X, predict_2, color='green', label='max_depth=2')
plt.title('Decision Tree Regression')
plt.xlabel('Egitim Seviyesi')
plt.ylabel('Maas')
plt.legend()
plt.show()

decision tree regression plot 2

Evaluation

Görüldüğü üzere max_depth=None değeri ağacın yaprak sayısı saf olana kadar devam etmiş ve daha doğru sonuçlar vermiştir.

max_depth=None olarak ayarlanmasının nedeni, karar ağacının maksimum derinliğinin sınırsız bırakılmasıdır. Bu, ağacın her yaprak düğüm saf olana (yani tek bir sınıf veya değere sahip olana) veya düğümler minimum örnek sayısına ulaşana kadar (diğer parametreler tarafından belirlenir) büyümesine izin verir.

Bu yaklaşımın birkaç avantajı ve dezavantajı vardır:

Avantajlar

1. Tam Uyum Sağlama:

Karar ağacı, verideki tüm örüntüleri tam olarak öğrenebilir. Bu, modelin eğitim verisi üzerinde çok iyi performans göstermesine neden olabilir, çünkü her karar düğümü, verinin mümkün olan en iyi şekilde bölünmesine izin verir.

2. Tüm Verileri Kullanma:

Derinliğin sınırsız bırakılması, karar ağacının verideki en küçük varyasyonları bile yakalamasını sağlar. Bu, modelin esneklik ve duyarlılığını artırabilir.

Dezavantajlar

1. Aşırı Öğrenme (Overfitting):

Ağaç çok derin olduğunda, eğitim verisine tam olarak uyum sağlar, bu da aşırı öğrenmeye neden olabilir. Aşırı öğrenme, modelin eğitim verisinde çok iyi performans gösterirken, yeni (görülmemiş) verilerde zayıf performans göstermesine yol açar.

2. Karmaşık Modeller:

Çok derin ağaçlar, çok fazla düğüm ve yaprak içerebilir, bu da modelin yorumlanabilirliğini zorlaştırır. Ayrıca, karmaşık modeller daha yavaş çalışabilir ve daha fazla hesaplama kaynağı gerektirebilir.

3. Genelleme Kapasitesinin Azalması:

Çok fazla derinleşen ağaçlar, veri kümesindeki gürültüyü öğrenme riski taşır. Bu, modelin genelleme kapasitesini azaltabilir ve yeni verilerle karşılaştığında beklenmedik sonuçlar vermesine neden olabilir.

Uygulama Sebepleri

  • Deneme Aşamasında: Modeli geliştirme aşamasında max_depth=None bırakmak, modelin veri üzerinde nasıl çalıştığını görmek için yararlı olabilir. Bu, modelin doğal derinliğini anlamanızı ve daha sonra bu derinliği sınırlamak için uygun bir değer seçmenize yardımcı olabilir.
  • Küçük ve Basit Veri Setlerinde: Eğer veri seti küçük ve özellik sayısı sınırlıysa, aşırı derinlik sorunu olmadan max_depth=None bırakılabilir. Bu durumlarda model, doğal olarak uygun derinlikte bir ağaç oluşturabilir.

Sonuç olarak, max_depth=None parametresi, ağaç derinliğini sınırsız bırakarak modelin veri üzerinde maksimum esneklikle çalışmasına olanak tanır, ancak aşırı öğrenme riskini artırır. Bu nedenle, uygulamada bu parametreyi dikkatli bir şekilde ayarlamak ve gerekirse çapraz doğrulama gibi tekniklerle doğru derinliği seçmek önemlidir.