Support Vector Regression (SVR) Example
Bu yazıda da eğitim seviyesi ile maaş miktarı arasındaki ilişkiyi inceleyen bir support vector regression modelini ele alacağız.
- 1. Doğrusal (Linear) SVR
- 2. Polinomal (Polynomial) SVR
- 3. Radial Basis Function (RBF) SVR
- 4. Sigmoid SVR
- Dataset
- Import Libraries
- Data Preprocessing
- Building and Training Model
- Predict
- Visualization
Support Vector Regression (SVR), Makine Öğrenimi alanında kullanılan bir regresyon tekniğidir ve Support Vector Machines (SVM) prensiplerine dayanır.
SVR, SVM’in sınıflandırma problemlerinde kullanıldığı gibi, sürekli bir çıktıyı tahmin etmek için kullanılır.
SVR’in amacı, bir hiper düzlem oluşturmak ve bu düzlemden belirli bir mesafe içinde kalan veri noktalarını dikkate alarak regresyon yapmak, yani bir fonksiyonun tahminini gerçekleştirmektir.
SVR’nin temel bileşenleri şunlardır:
- Hata Marjı (ε-tüpü): SVR, verilerin üzerinde bir “tüp” (epsilon-tube) tanımlar ve bu tüpün içinde kalan hataları görmezden gelir. Bu tüp, modelin ne kadar hassas olacağını belirler. Hedef, bu tüpün içinde mümkün olduğunca fazla veri noktası yerleştirerek bir fonksiyon elde etmektir.
- Destek Vektörleri: Tıpkı SVM’de olduğu gibi, SVR de yalnızca destek vektörleri olarak adlandırılan kritik veri noktalarına dayanır. Bu noktalar, tüpün sınırında veya dışında yer alır ve modelin hiper düzleminin konumunu belirler.
- C Parametresi: C parametresi, modelin karmaşıklığını kontrol eder. Daha büyük bir C değeri, modelin daha fazla veri noktasını tam olarak tahmin etmesini sağlar (daha az hata), ancak bu durum modelin aşırı öğrenmesine (overfitting) neden olabilir.
- Kernel Fonksiyonu: SVR, doğrusal olmayan verilerle çalışabilmek için kernel fonksiyonları kullanır. RBF (Radial Basis Function), polynomial ve sigmoid kernel fonksiyonları yaygın olarak kullanılır. Kernel fonksiyonu, verileri daha yüksek boyutlu bir uzaya projelendirerek, doğrusal olmayan ilişkilerin modellenmesini sağlar.
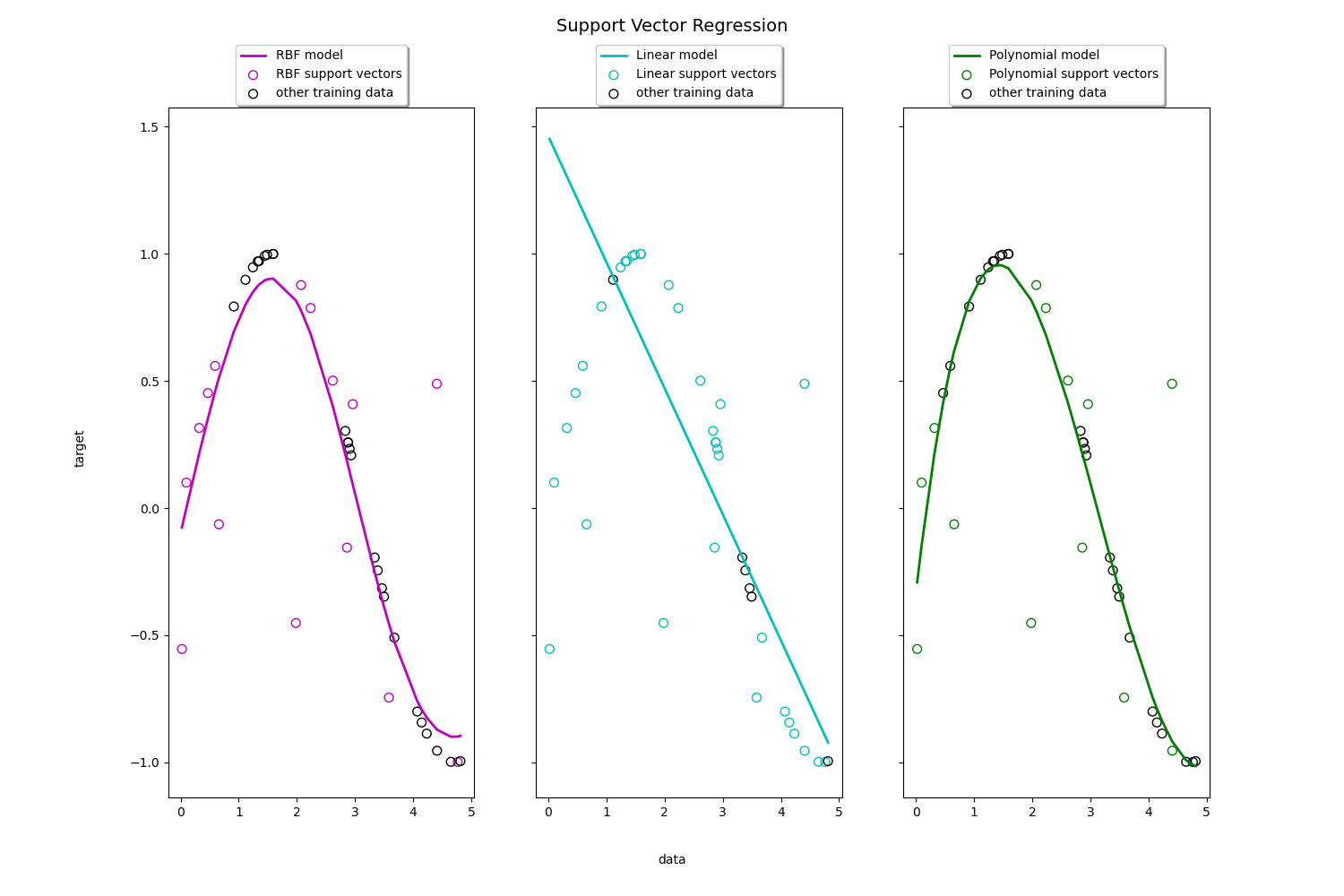
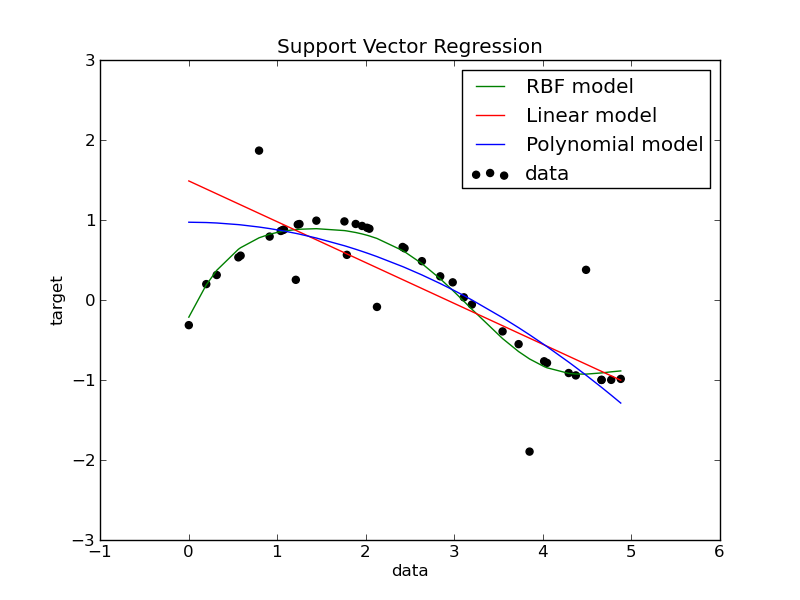
Support Vector Regression (SVR), genellikle kullanılan çekirdek (kernel) fonksiyonlarına göre sınıflandırılır. Çekirdek fonksiyonları, verileri daha yüksek boyutlu bir uzaya projelendirerek doğrusal olmayan ilişkilerin modellenmesini sağlar.
1. Doğrusal (Linear) SVR
- Açıklama : Doğrusal çekirdek fonksiyonu kullanır ve verilerin doğrusal bir şekilde ayrılabileceği varsayımıyla çalışır. Veriler arasındaki ilişki doğrusal olduğunda tercih edilir.
- Çekirdek Fonksiyonu : \(K(x_i, x_j) = x_i * x_j\)
- Uygulama Alanı : Yüksek boyutlu ama doğrusal ayrılabilir veri setlerinde kullanılır.
2. Polinomal (Polynomial) SVR
- Açıklama : Veriler arasındaki doğrusal olmayan ilişkileri modellemek için polinomal bir çekirdek fonksiyonu kullanır. Polinomal derecesi, modelin karmaşıklığını kontrol eder.
- Çekirdek Fonksiyonu : \(K(x_i, x_j) = (x_i * x_j + c) ^ d\)
Burada \(c\) bir sabit ve \(d\) polinomun derecesidir.
- Uygulama Alanı : Doğrusal olmayan ilişkilerin var olduğu veri setlerinde kullanılır, özellikle daha karmaşık ilişkileri modellemek için.
3. Radial Basis Function (RBF) SVR
- Açıklama : En yaygın kullanılan çekirdek fonksiyonlarından biridir. RBF çekirdeği, verileri sonsuz boyutlu bir uzaya projelendirerek çok karmaşık doğrusal olmayan ilişkileri modelleyebilir.
- Çekirdek Fonksiyonu : \(K(x_i, x_j) = exp(-γ \| x_i - x_j \| ^ 2)\)
Burada γ parametresi, kernelin genişliğini kontrol eder.
4. Sigmoid SVR
- Açıklama : Sinir ağlarındaki aktivasyon fonksiyonuna benzer bir çekirdek fonksiyonu kullanır. Bu çekirdek fonksiyonu doğrusal olmayan ilişkileri modellemek için uygundur, ancak genellikle belirli uygulamalarda kullanılır.
- Çekirdek Fonksiyonu : \(K(x_i, x_j) = tanh(ax_i * x_j + c)\)
Burada a ve c çekirdek parametreleridir.
- Uygulama Alanı : Özellikle belirli biyolojik veya sinirsel veri modellemelerinde kullanılabilir.
Dataset
Import Libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sbn
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
Data Preprocessing
Read Data
data = pd.read_csv('salaries.csv')
print(data)
unvan Egitim Seviyesi maas
0 Cayci 1 2250
1 Sekreter 2 2500
2 Uzman Yardimcisi 3 3000
3 Uzman 4 4000
4 Proje Yoneticisi 5 5500
5 Sef 6 7500
6 Mudur 7 10000
7 Direktor 8 15000
8 C-level 9 25000
9 CEO 10 50000
Graphical Analysis of Data
sbn.pairplot(data)
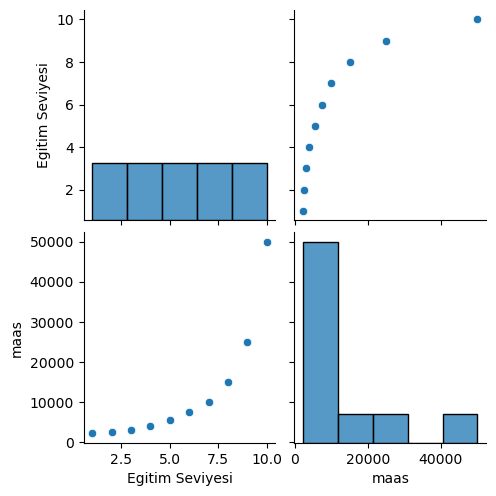
print(data.describe())
Egitim Seviyesi maas
count 10.00000 10.000000
mean 5.50000 12475.000000
std 3.02765 14968.694183
min 1.00000 2250.000000
25% 3.25000 3250.000000
50% 5.50000 6500.000000
75% 7.75000 13750.000000
max 10.00000 50000.000000
Split Data
egitim_seviyesi = data.iloc[:,1:2].values
maas = data.iloc[:,2:].values
Scaling
Support Vector Regression (SVR) ile çalışırken scaling (ölçeklendirme) işlemi yapılması gereklidir. Bunun başlıca nedenleri:
1. SVR’nin Çekirdek Fonksiyonları ile Uyum
- Çoğu SVR modeli, RBF (Radial Basis Function) ve polynomial gibi çekirdek fonksiyonları kullanır. Bu çekirdek fonksiyonları, özellikler arasındaki mesafelere dayalı olarak çalışır. Eğer özellikler farklı ölçeklerdeyse (örneğin biri 0-1 arasında, diğeri 1-1000 arasında), bu durum SVR’nin performansını olumsuz etkileyebilir çünkü daha büyük ölçekli özellikler modelde daha fazla ağırlık kazanır.
2. Optimizasyonun Daha Kolay Yapılması
- SVR, optimizasyon sürecinde \(C\) (regülarizasyon parametresi) ve \(γ\) (gamma) gibi hiperparametreleri kullanır. Özelliklerin ölçeklenmesi bu hiperparametrelerin daha etkili bir şekilde ayarlanmasını sağlar ve optimizasyon sürecini daha kararlı hale getirir.
3. Hızlı ve Stabil Hesaplama
- Özellikler ölçeklenmediğinde, SVR’nin hesaplama süresi uzayabilir ve modelin çözümünde kararsızlıklar meydana gelebilir. Özelliklerin ölçeklenmesi hesaplamaların daha hızlı ve stabil olmasını sağlar.
Özetle, SVR ile çalışırken, özelliklerin ölçeklendirilmesi kritik bir adımdır ve genellikle model performansını optimize etmek için gereklidir. Bu nedenle, SVR’yi uygulamadan önce mutlaka veriler ölçeklendirilmelidir.
sc1 = StandardScaler()
egitim_seviyesi_scale = sc1.fit_transform(egitim_seviyesi)
sc2 = StandardScaler()
maas_scale = sc2.fit_transform(maas)
Building and Training Model
Şimdi RBF kernel fonksiyonu ile bir SVR objesi oluşturalım. Kernel fonksiyonu olarak;
linearpolysigmoidprecomputed
fonksiyonlarından birini de seçebilirdik. Hangi çekirdek fonksiyonunun kullanılacağı, verilerin doğasına ve modelin doğrusal olmayan ilişkileri ne kadar iyi yakalayabileceğine bağlı olarak seçilmelidir.
svr_reg = SVR(kernel='rbf', degree=3, gamma='scale',C=1.0, epsilon=0.1)
# degree, gamma, C ve epsilon parametrelerine tanımlı olan değerler default değerlerdir. Bu parametreler verilmezsede olur.
svr_reg.fit(egitim_seviyesi_scale, maas_scale)
Predict
maas_predict = svr_reg.predict(egitim_seviyesi_scale)
for i in range(len(maas_scale)):
print('Gerçek Maaş: ', maas_scale[i], '\tTahmin Maaş: ', maas_predict[i])
Gerçek Maaş: [-0.72004253] Tahmin Maaş: -0.6198571722381288
Gerçek Maaş: [-0.70243757] Tahmin Maaş: -0.6290330048896189
Gerçek Maaş: [-0.66722767] Tahmin Maaş: -0.5673565753924996
Gerçek Maaş: [-0.59680786] Tahmin Maaş: -0.4966225171862582
Gerçek Maaş: [-0.49117815] Tahmin Maaş: -0.446305638990747
Gerçek Maaş: [-0.35033854] Tahmin Maaş: -0.36590426720699826
Gerçek Maaş: [-0.17428902] Tahmin Maaş: -0.14129747801052855
Gerçek Maaş: [0.17781001] Tahmin Maaş: 0.2851025834244593
Gerçek Maaş: [0.88200808] Tahmin Maaş: 0.7816373730639689
Gerçek Maaş: [2.64250325] Tahmin Maaş: 1.0850064515089588
Görüldüğü üzere oluşturmuş olduğumuz SVR modeli makul seviyede tahminler yaptı.
Buradaki tahmin sonuçları scale edilmiş bir verisetinin sonuçları olduğu için bu sonuçlar olması gereken ölçekte değiller. Eğer elde edilen bu tahmin sonuçlarını olması gereken ölçeğe geri getirmek istiyorsak, tahmin edilen değerlerin ters ölçeklenmesi gerekir.
Visualization
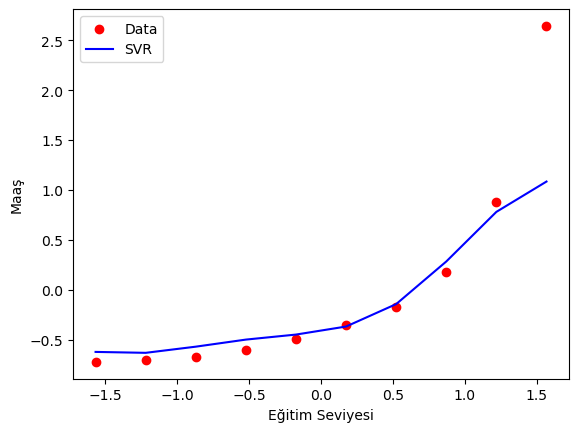
plt.scatter(egitim_seviyesi_scale, maas_scale, color='red', label='Data')
plt.plot(egitim_seviyesi_scale, maas_predict, color='blue', label = 'SVR')
plt.xlabel('Eğitim Seviyesi')
plt.ylabel('Maaş')
plt.legend()
plt.show()