Polynomial Regression Example
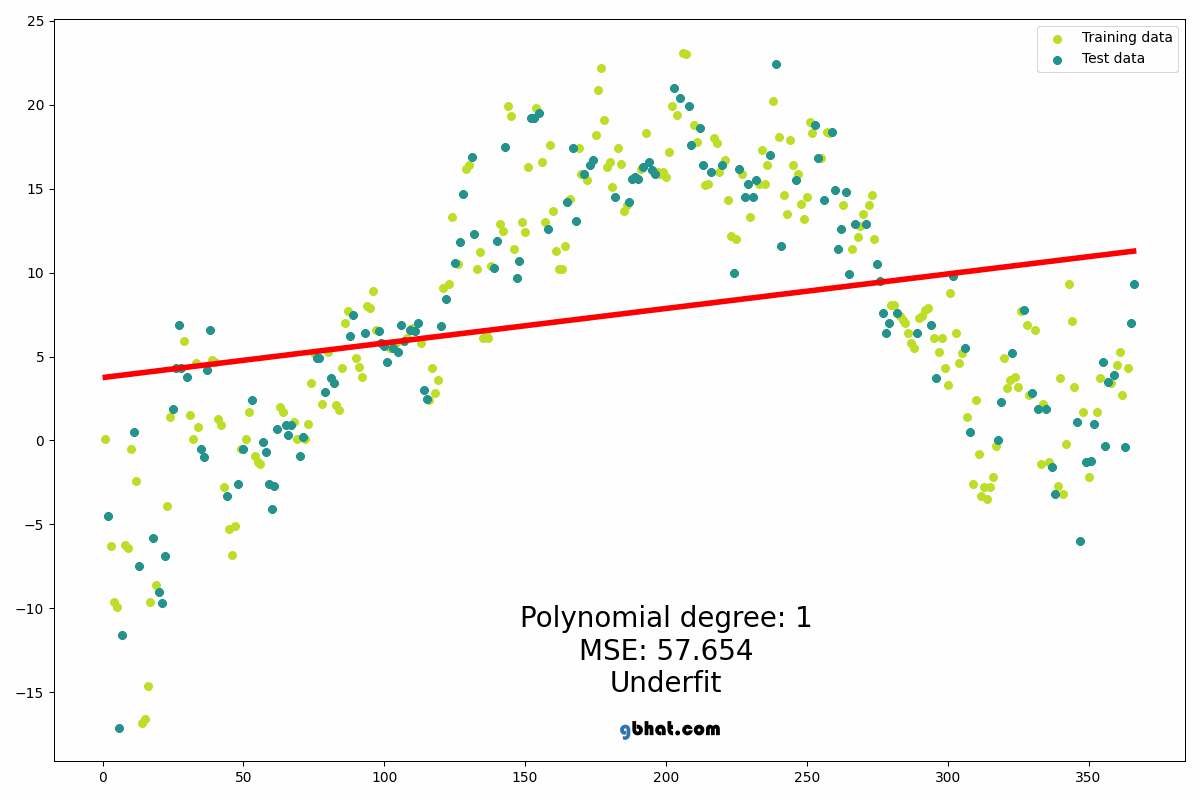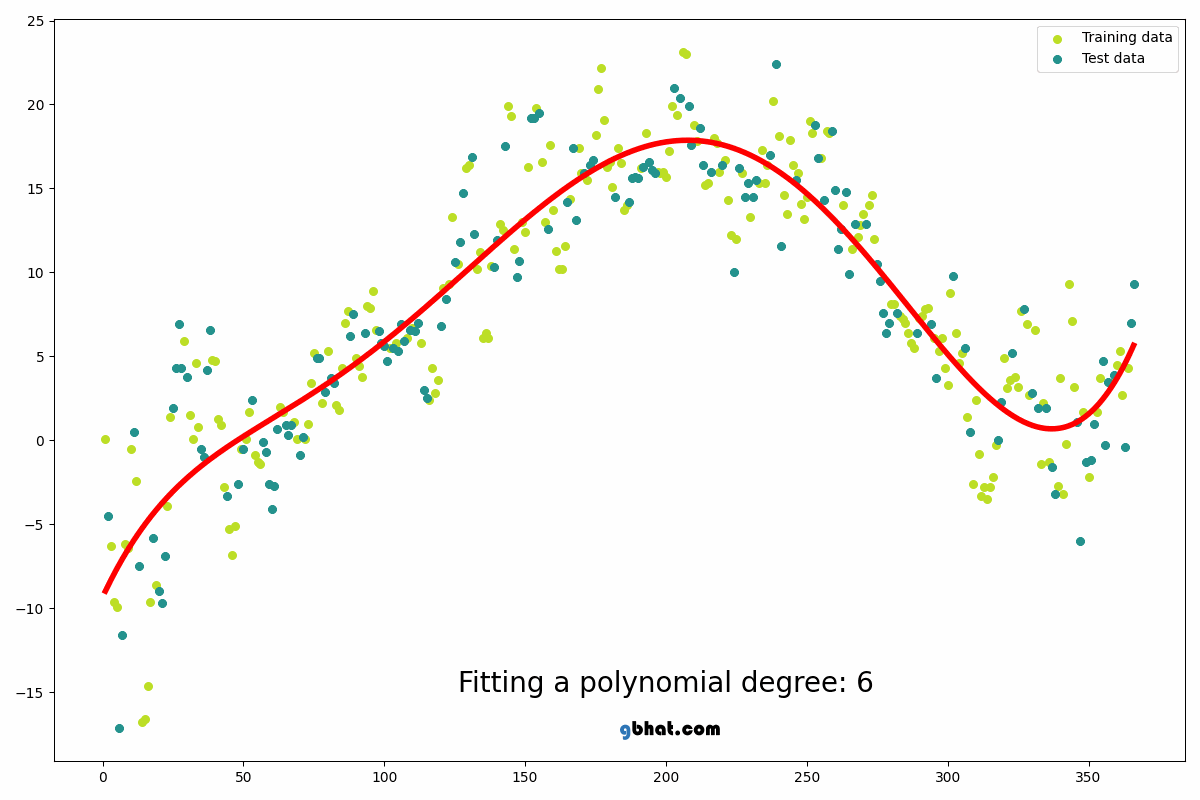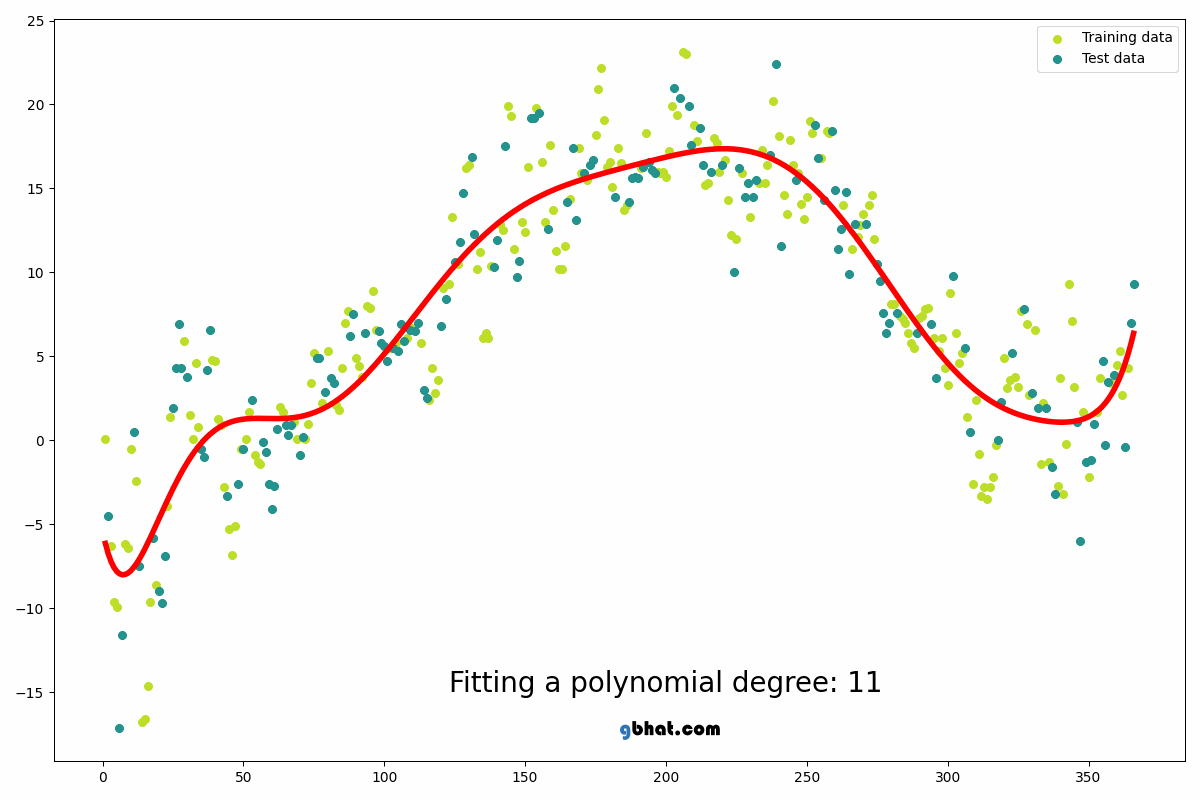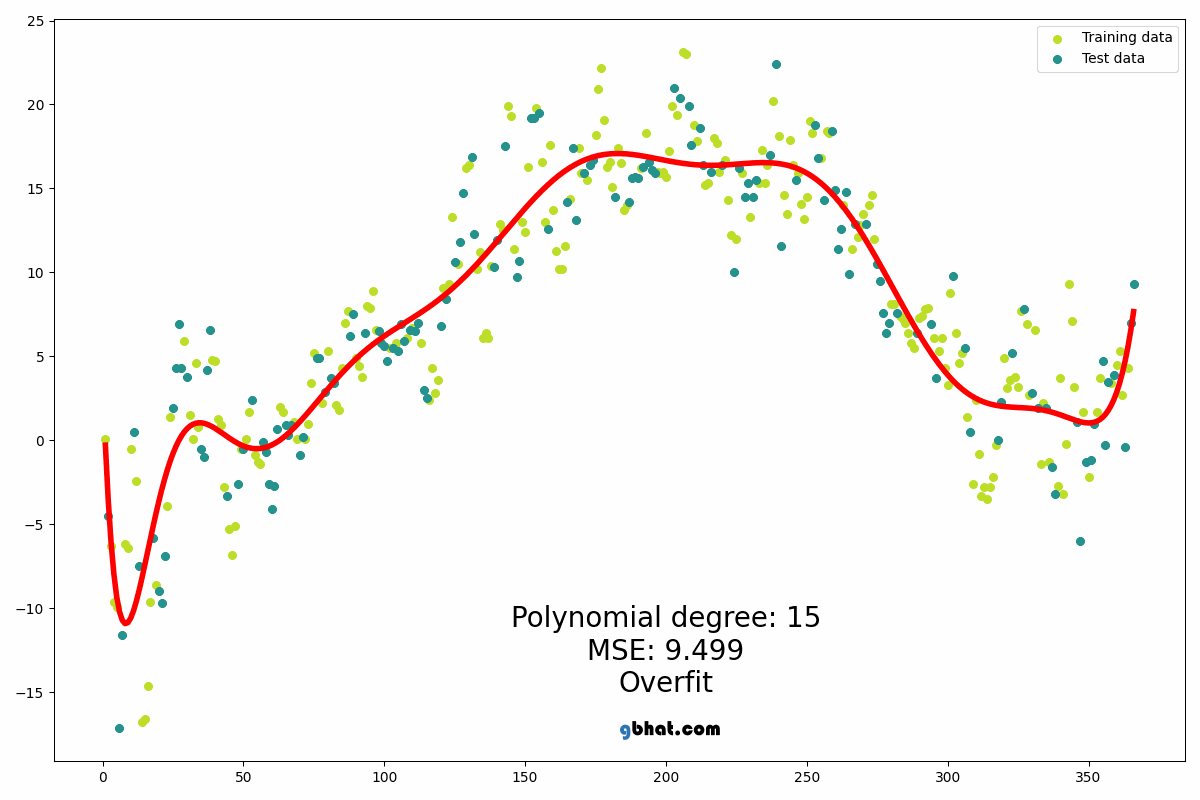
Bu yazıda da eğitim seviyesi ile maaş miktarı arasındaki ilişkiyi inceleyen bir polynomial regression modelini ele alacağız.
Bu modelde, bağımsız değişkenler üzerindeki polinom terimleri (x, x², x³, vb.) eklenir. Bu sayede, verideki doğrusal olmayan ilişkiler yakalanabilir. \[y= β_0 + β_1 x_1 + β_2 x_2^2 + … + β_n x_n^n\]
Örneğin, doğrusal regresyon (lineer regresyon) bir veriyi düz bir çizgi ile modellemeye çalışırken, polynomial regresyon bu çizgiyi eğrilerle modelleyebilir. Bu özellikle verilerdeki karmaşık desenleri daha iyi yakalamak için faydalıdır.
Bu yazıda da eğitim seviyesi ile maaş miktarı arasındaki ilişkiyi inceleyen bir polynomial regression modelini ele alacağız.
Dataset
Import Libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sbn
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
Data Preprocessing
Read Data
data = pd.read_csv('salaries.csv')
print(data)
Graphical Analysis of Data
sbn.pairplot(data)
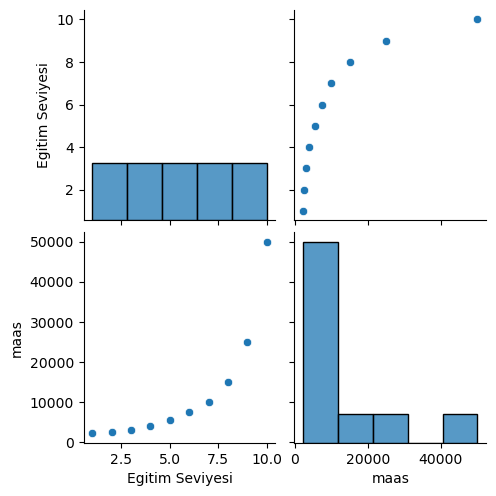
print(data.describe())
Egitim Seviyesi maas
count 10.00000 10.000000
mean 5.50000 12475.000000
std 3.02765 14968.694183
min 1.00000 2250.000000
25% 3.25000 3250.000000
50% 5.50000 6500.000000
75% 7.75000 13750.000000
max 10.00000 50000.000000
Split Data
egitim_seviyesi = data.iloc[:,1:2].values
maas = data.iloc[:,2:].values
Polynomial Regression
poly_reg = PolynomialFeatures(degree = 2)
egitim_seviyesi_poly = poly_reg.fit_transform(egitim_seviyesi)
print(egitim_seviyesi_poly)
[[ 1. 1. 1.]
[ 1. 2. 4.]
[ 1. 3. 9.]
[ 1. 4. 16.]
[ 1. 5. 25.]
[ 1. 6. 36.]
[ 1. 7. 49.]
[ 1. 8. 64.]
[ 1. 9. 81.]
[ 1. 10. 100.]]
PolynomialFeatures sınıfındaki degree parametresi, oluşturulacak olan polinomun derecesini belirler.
Bu parametre, modelin karmaşıklığını ve eğitim verilerindeki doğrusal olmayan ilişkileri yakalama kapasitesini doğrudan etkiler.
degree parametresi, aşağıdaki faktörlere göre ayarlanır:
- Verinin Doğası ve Karmaşıklığı : Verinin içerdiği ilişkilere bağlı olarak daha yüksek dereceli polinomlar (örneğin
degree=3veyadegree=4) daha karmaşık ilişkileri modelleyebilir. Ancak, derece arttıkça modelin aşırı uyum (overfitting) yapma riski de artar. - Model Karmaşıklığı ve Genelleme Yeteneği : Yüksek dereceli polinomlar, eğitim verilerine çok iyi uyabilir, ancak bu durumda model genelleme yeteneğini kaybedebilir. Genellikle düşük dereceler (örneğin
degree=2) daha basit ve genelleyici modeller sağlar. - Deneysel Değerlendirme ve Doğrulama : Farklı dereceler için model performansı çapraz doğrulama (cross-validation) ile değerlendirilebilir. Bu sayede, veri seti üzerinde en iyi performansı gösteren
degreedeğeri seçilebilir. - Veri Miktarı ve Gürültü : Az sayıda veri veya yüksek gürültü içeren veri setlerinde, düşük dereceli polinomlar tercih edilebilir, çünkü bu durumda yüksek dereceler gürültüyü modelleyerek hatalı sonuçlara yol açabilir.
Train and Predict
lin_reg = LinearRegression()
lin_reg.fit(egitim_seviyesi_poly,maas)
maas_predict = lin_reg.predict(egitim_seviyesi_poly)
for i in range(len(maas_predict)):
print("Eğitim seviyesi", egitim_seviyesi[i], "\tGerçek Maaş : ", maas[i], "\tPolynomial Maaş : ", maas_predict[i])
Eğitim seviyesi [1] Gerçek Maaş : [2250] Polynomial Maaş : [5936.36363636]
Eğitim seviyesi [2] Gerçek Maaş : [2500] Polynomial Maaş : [2207.57575758]
Eğitim seviyesi [3] Gerçek Maaş : [3000] Polynomial Maaş : [421.96969697]
Eğitim seviyesi [4] Gerçek Maaş : [4000] Polynomial Maaş : [579.54545455]
Eğitim seviyesi [5] Gerçek Maaş : [5500] Polynomial Maaş : [2680.3030303]
Eğitim seviyesi [6] Gerçek Maaş : [7500] Polynomial Maaş : [6724.24242424]
Eğitim seviyesi [7] Gerçek Maaş : [10000] Polynomial Maaş : [12711.36363636]
Eğitim seviyesi [8] Gerçek Maaş : [15000] Polynomial Maaş : [20641.66666667]
Eğitim seviyesi [9] Gerçek Maaş : [25000] Polynomial Maaş : [30515.15151515]
Eğitim seviyesi [10] Gerçek Maaş : [50000] Polynomial Maaş : [42331.81818182]
Visualize Results
plt.scatter(egitim_seviyesi,maas,color='red', label = 'Data')
plt.plot(egitim_seviyesi,maas_predict,color='blue', label = 'Poly')
plt.xlabel('Egitim Seviyesi')
plt.ylabel('Maas')
plt.legend()
plt.show()
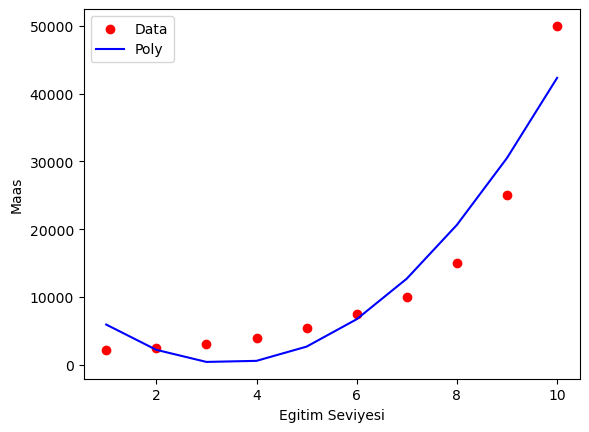
Şimdi dereceyi arttıralım ve modeli oluşturup tekrar train edelim.
poly_reg = PolynomialFeatures(degree = 4)
egitim_seviyesi_poly = poly_reg.fit_transform(egitim_seviyesi)
print(egitim_seviyesi_poly)
[[1.000e+00 1.000e+00 1.000e+00 1.000e+00 1.000e+00]
[1.000e+00 2.000e+00 4.000e+00 8.000e+00 1.600e+01]
[1.000e+00 3.000e+00 9.000e+00 2.700e+01 8.100e+01]
[1.000e+00 4.000e+00 1.600e+01 6.400e+01 2.560e+02]
[1.000e+00 5.000e+00 2.500e+01 1.250e+02 6.250e+02]
[1.000e+00 6.000e+00 3.600e+01 2.160e+02 1.296e+03]
[1.000e+00 7.000e+00 4.900e+01 3.430e+02 2.401e+03]
[1.000e+00 8.000e+00 6.400e+01 5.120e+02 4.096e+03]
[1.000e+00 9.000e+00 8.100e+01 7.290e+02 6.561e+03]
[1.000e+00 1.000e+01 1.000e+02 1.000e+03 1.000e+04]]
lin_reg = LinearRegression()
lin_reg.fit(egitim_seviyesi_poly,maas)
maas_predict = lin_reg.predict(egitim_seviyesi_poly)
for i in range(len(maas_predict)):
print("Eğitim seviyesi", egitim_seviyesi[i], "\tGerçek Maaş : ", maas[i], "\tPolynomial Maaş : ", maas_predict[i])
Eğitim seviyesi [1] Gerçek Maaş : [2250] Polynomial Maaş : [2667.83216783]
Eğitim seviyesi [2] Gerçek Maaş : [2500] Polynomial Maaş : [1587.99533799]
Eğitim seviyesi [3] Gerçek Maaş : [3000] Polynomial Maaş : [2932.1095571]
Eğitim seviyesi [4] Gerçek Maaş : [4000] Polynomial Maaş : [4731.64335664]
Eğitim seviyesi [5] Gerçek Maaş : [5500] Polynomial Maaş : [6086.24708625]
Eğitim seviyesi [6] Gerçek Maaş : [7500] Polynomial Maaş : [7163.75291375]
Eğitim seviyesi [7] Gerçek Maaş : [10000] Polynomial Maaş : [9200.17482518]
Eğitim seviyesi [8] Gerçek Maaş : [15000] Polynomial Maaş : [14499.70862471]
Eğitim seviyesi [9] Gerçek Maaş : [25000] Polynomial Maaş : [26434.73193474]
Eğitim seviyesi [10] Gerçek Maaş : [50000] Polynomial Maaş : [49445.80419581]
plt.scatter(egitim_seviyesi,maas,color='red', label = 'Data')
plt.plot(egitim_seviyesi,maas_predict,color='blue', label = 'Poly')
plt.xlabel('Egitim Seviyesi')
plt.ylabel('Maas')
plt.legend()
plt.show()
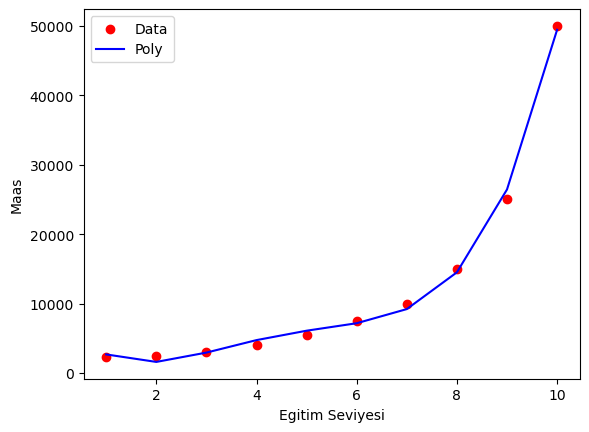
Grafikten de anlaşılacağı üzere 4. derece bir polynomial regression modeli daha iyi bir sonuç verdi.